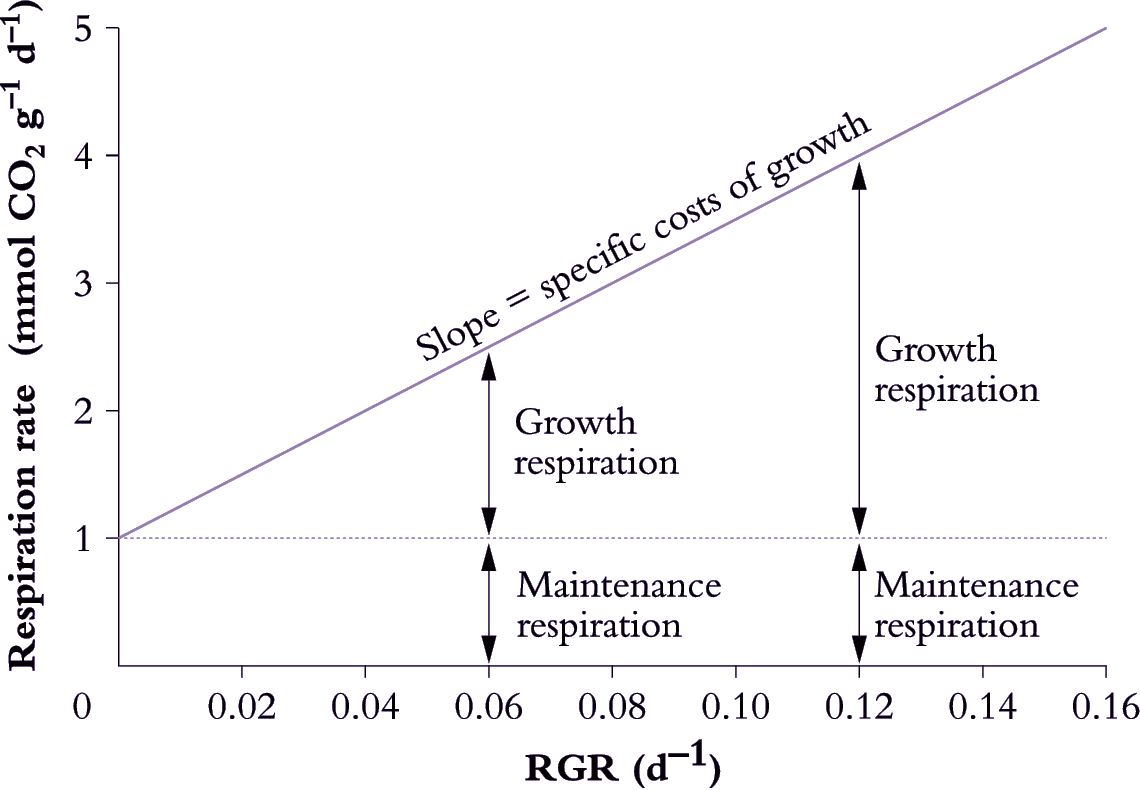
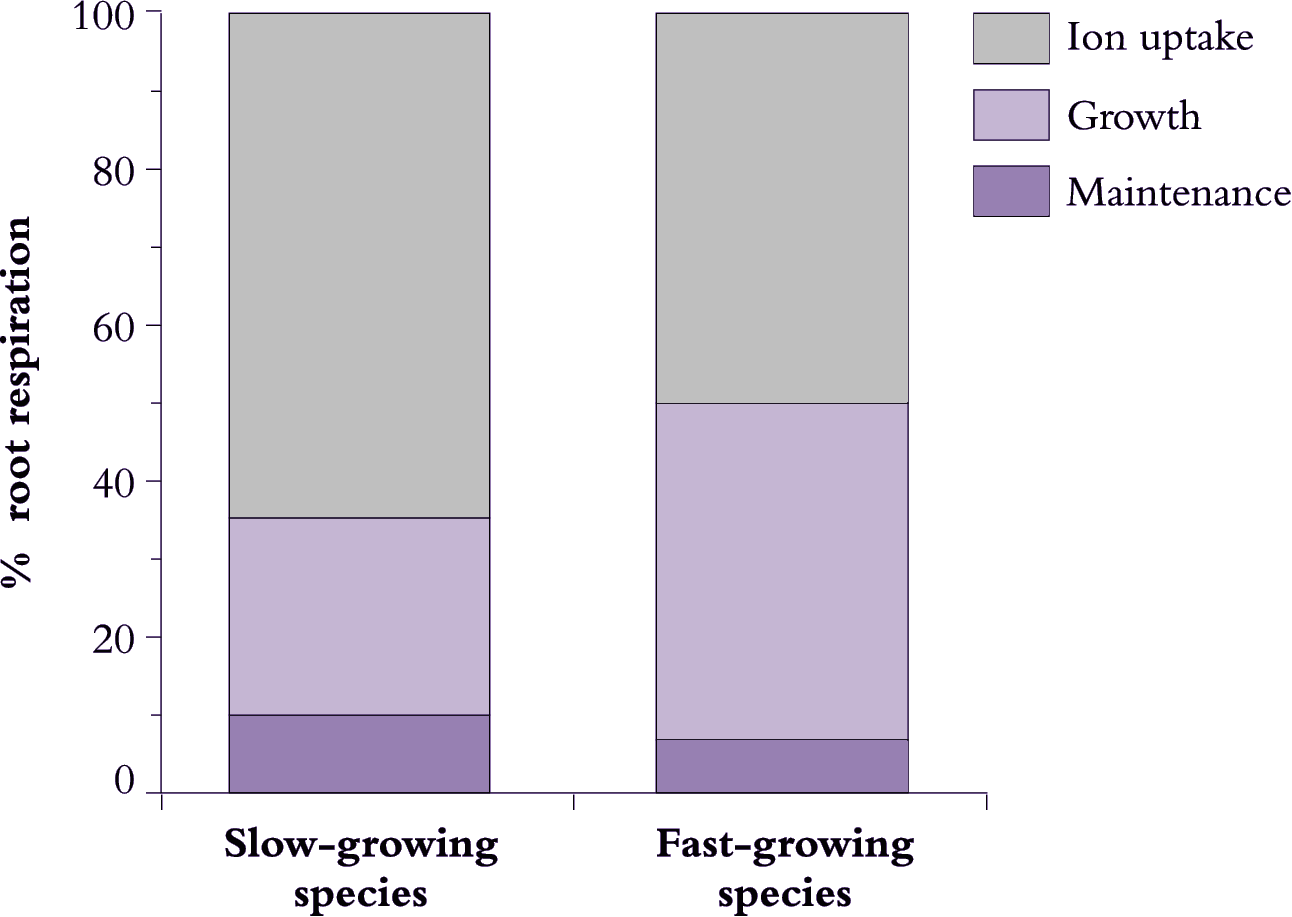Growth respiration can be distinguished from maintenance respiration by relating variation in respiration rate to variation in RGR over short time intervals (Figure 6.19; Penning de Vries 1975). This approach assumes a model for respiration where:
\[\text{Total respiration} = \text{Maintenance respiration} + \text{(Specific costs of growth} \times \text {RGR)} \tag{6.31}\]
where respiration is expressed in mmol CO2 g-1 d-1, and specific costs of growth in mmol CO2 g-1.
Decreases in RGR (e.g. due to growth under different irradiance or during ageing) are assumed to decrease demand for growth respiration, whereas demand for maintenance respiration is assumed to remain constant at different RGR values. Based on these assumptions, the maintenance component can be estimated by extrapolating the respiration rate back to a point where no growth occurs (1 mmol CO2 g–1 d–1 in Figure 6.19). Specific respiratory costs associated with growth can be estimated from the slope of the respiration–RGR plot (25 mmol CO2 g–1 in Figure 6.19).
An alternative approach to maintenance and growth components of respiration involves holding plants in extended darkness. Most annual plants use up their readily available energy sources after about 2 d and shoot growth will cease. Rate of CO2 release would then reflect the maintenance component of dark respiration. The difference in dark respiration rates before and after 2 d darkness would be the growth component.
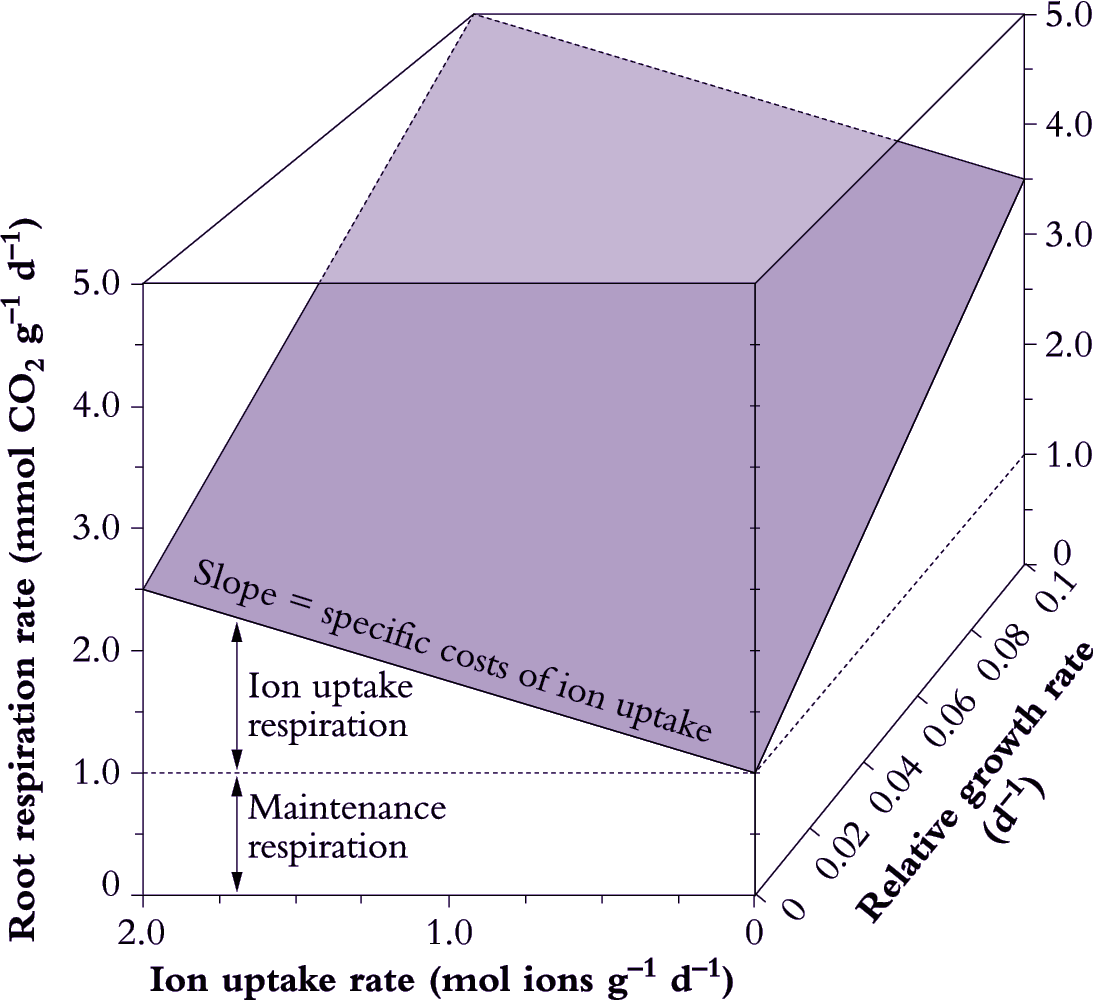
Such methods incorporate specific costs of ion uptake into estimates of growth respiration, but do not isolate the ion uptake component of root respiration. Ion uptake respiration can be separated from growth by partitioning root respiration into growth, maintenance and ion uptake components. The approach adopted by Veen (1980) assumes a model where:
\[\text{Root respiration} = \text{Maintenance respiration} + \text{(Specific costs of growth} \times \text {RGR)} + \text{(Specific costs of ion uptake} \times \text{Ion uptake rate)} \tag{6.31}\]
A multiple regression analysis approach can be used to separate these components (Figure 6.20). Root respiration is taken as a dependent variable; while RGR and ion uptake rate are independent variables (van der Werf et al. 1994). The maintenance component of root respiration is taken as the rate of respiration when growth and ion uptake are extrapolated back to zero. Specific costs of growth and ion uptake are taken as the slope of the respiration versus growth and ion uptake regressions, respectively.
Most respiratory energy is allocated to nutrient acquisition in both fast- and slow-growing species (Figure 6.21) and this proportion increases even further under suboptimal conditions as maintenance costs rise. However, fast-growing species are distinguished by allocating less respiratory energy to nutrient acquisition, and more to growth. Presumably, a lower allocation to ion uptake in fast-growing species arises from lower specific costs. Loss of absorbed nutrients could also be lower in fast-growing species, while cotransport of protons and anions into roots might conserve energy. Maintenance costs also appear to be slightly lower in fast-growing plants (Figure 6.21) but any difference between these two plant categories in allocation to maintenance processes is small and is unlikely to matter overall. Nevertheless, differences in maintenance respiration will become more important when a plant is exposed to unfavourable conditions which invariably increase allocation of respiratory energy to fine-root turnover and maintenance of those structures.