Enzymes play a major role in regulating the way in which plants respond to temperature. The effect of temperature on enzyme activity is expressed through the maximum rate (Vmax) and the enzyme–substrate affinity (Km) and this in turn is related to the effect of temperature on enzyme synthesis, activation and stability.
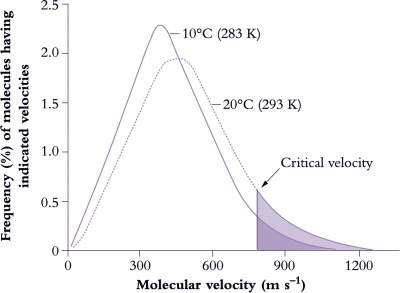
Basic metabolic rates tend to increase exponentially within their dynamic range (10–30°C) so that a rise in temperature of 10°C will at least double reaction rate, that is, ‘Q10’ = 2 (Figure 14.15). Q10 represents the net outcome of increased activity of an enzyme system with increased temperature, offset by any deactivation of the enzyme associated with this increase. Q10 values for metabolic processes are generally in the range of 2–3 and values below this imply that the reaction is at least partly governed by physical rather than metabolic processes. Q10 values for physical processes are commonly around 1.3. Physical limitation occurs when there are barriers to the transfer of substrate to reaction sites in a cell. Reaction rates of whole organisms or even organs often increase approximately linearly with temperature. Respiration is a case in point. This departure from an exponential increase results from a progressive shift in the reaction rates of component processes which first increase exponentially with temperature but then become modified by physical constraints such as substrate availability.
Enzymes can adjust to changes in the temperature environment, such that rates in acclimated plants are not as divergent as would be anticipated from the immediate response to temperature change. Acclimation can take a number of forms which may involve changes in isozymes or enzyme concentration, modification of an enzyme by substrate and effectors, or changes in metabolic regulation.
The concept of Q10 values has been extended to complex cellular and even whole-plant functions and has been used to provide some insight into the nature of the factors limiting the response of plants to temperature.
The ‘thermal kinetic window’ is a concept that relates enzyme activity and optimal plant metabolism to the temperature characteristics of the Michaelis–Menten constant (Km) of substrates and cofactors. Thermal kinetic windows define the temperature range outside which plants experience thermal stress. Many enzymes operate under non-saturating substrate concentrations and substrate binding (Km) may at times be of greater importance than maximum velocity (Vmax) for the characterisation of enzyme function under physiological conditions. The thermal kinetic window for a specific enzyme in a particular species (often spanning 8–15°C) is generally narrower than the plant temperatures experienced on a seasonal or daily basis, and temperature extremes that induce heat shock and chilling injury are not required for plants to experience some degree of thermal stress.
In the event of a sustained change in temperature conditions of plant growth, temperature:Km relationships for key enzyme reactions can adjust towards a temperature optimisation for metabolism and hence growth under those conditions, an out-come referred to above as acclimation and amenable to analysis via an Arrhenius plot to reveal underlying bioenergetics.
By analogy with graphs used to illustrate Michaelis–Menten kinetics, the natural logarithm of a physiological reaction rate (k) plotted against the reciprocal of absolute temperature (1/T) yields a straight line (Figure 14.7). This procedure in effect linearises an exponential response of reaction rate to temperature, and can be summarised in general terms as:
\[k=Ae^{\frac{E_a}{RT}}\tag{14.6}\]
where k is the rate constant of the reaction; A is a constant (exponential or frequency factor); Ea is the activation energy; R is the universal gas constant; T is absolute temperature in degrees Kelvin (K).
This equation can be rearranged to facilitate comparisons of reaction rate at two temperatures, T1 and T2:
\[\frac{\text{ln }k_2}{\text{ln }k_1} = A \frac{T_2-T_1}{T_1/T_2}\tag{14.7}\]
This relates enzyme activity to temperature where k1 and k2 are the reaction rates at absolute temperatures T1 and T2.
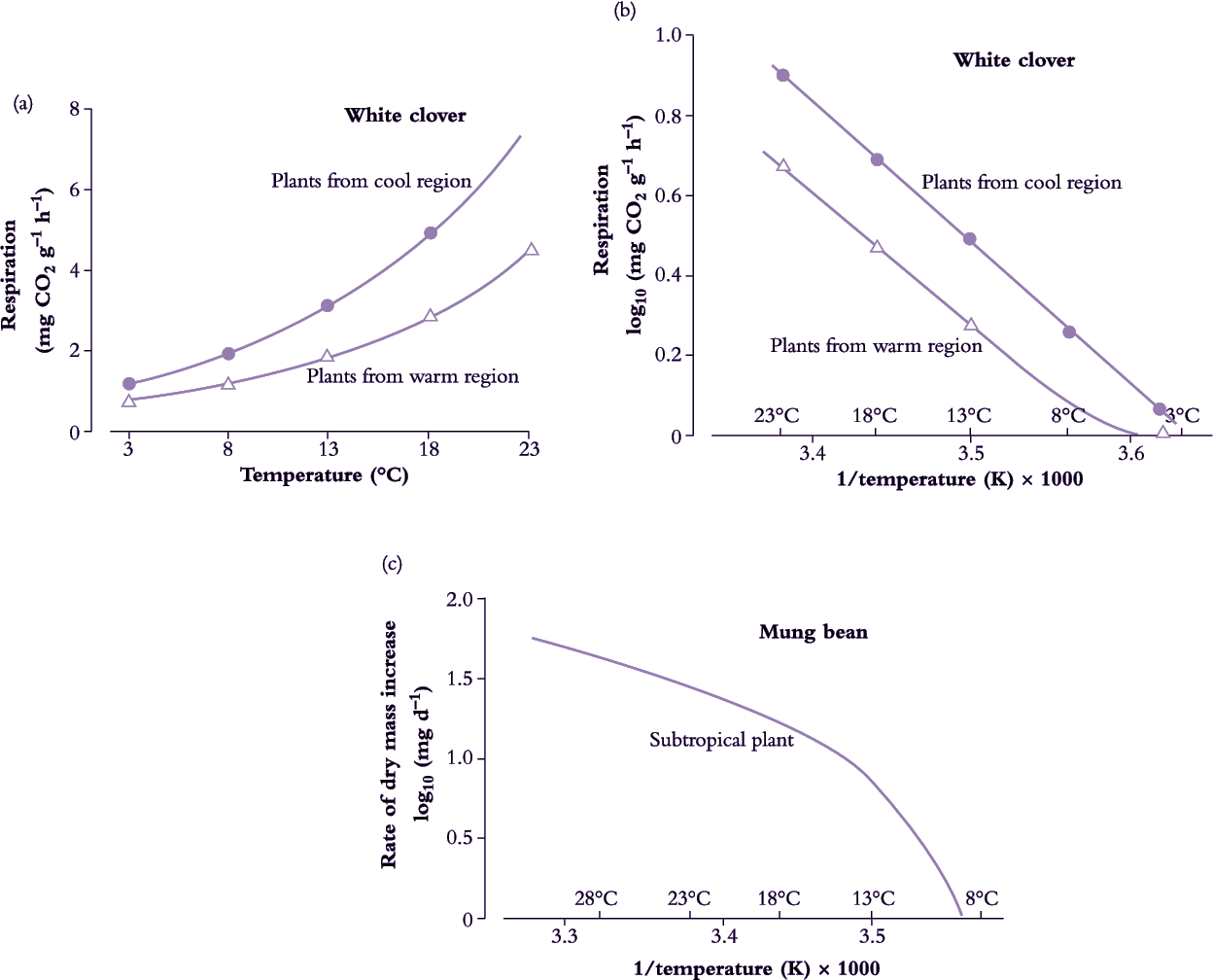
Plotting log k as a function of 1/T yields a linear relationship in the dynamic temperature range where the organism shows readily reversible responses to temperature, and can live indefinitely. Slope indicates the ‘energy of activation’ (Ea) which is the minimal energy required for the reaction to occur. A change in slope of this line indicates a change in sensitivity. A steeper slope at low temperature indicates that the energy of activation has increased and has therefore become more limiting to maximum velocity (Vmax) of the overall reaction (Figure 14.16).
Considerable use has been made of Arrhenius plots in attempts to determine critical temperatures for key enzymatic reactions in plant cells. Membrane lipids may undergo a phase change from the mobile to the solid state with a fall in temperature and this will vary with the nature of the lipids in the membrane, particularly the degree of unsaturation (double bonds). Any change in lipid properties would be expected to modify the activity of membrane-bound enzymes. Because of the complex nature of membranes, such change will often be a gradual rather than an abrupt change at a precise temperature.
Arrhenius plots have also been used to analyse the response to temperature of individual organs and whole plants in order to determine critical temperatures for growth. In chilling-sensitive species, the slope of the Arrhenius plot becomes steeper at low temperature, indicating a change in enzyme–temperature relationships. Plant taxa which experience broader ranges of temperature during growth in their native habitats can have smaller Arrhenius temperature coefficients.
Membranes and their associated enzymes are likely to provide a key to many temperature responses in plants and this can be extended to frost damage where membrane destabilisation resulting from freeze-induced dehydration is a major factor in freezing injury (Section 14.6).