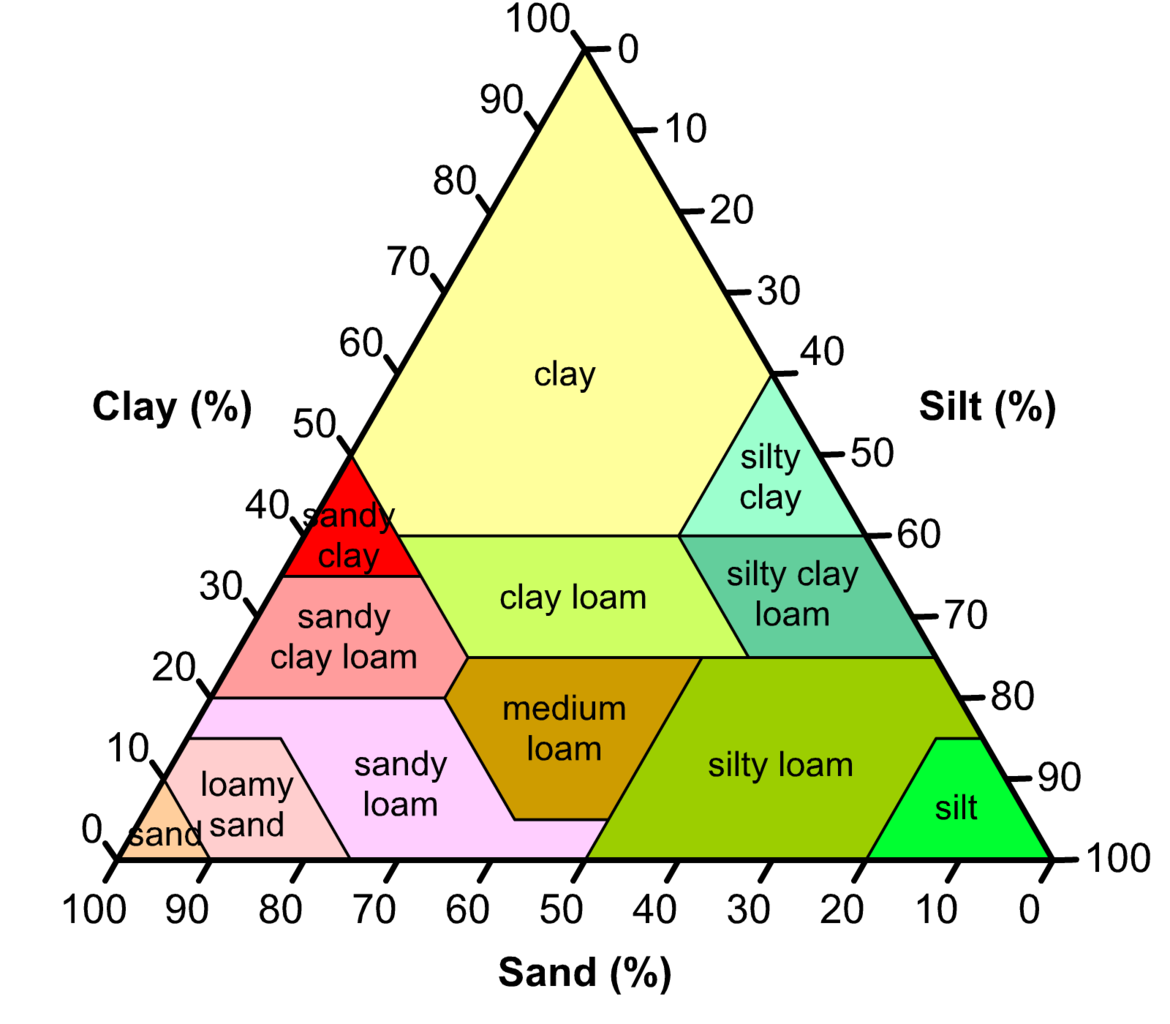
Figure 3.37 Textural classification of soils. Loam is a soil comprised of roughly equal amounts of sand and silt and a little less clay. http://imgkid.com/soil-texture-triangle.shtml
Plants lose water by evaporation through their leaves to the atmosphere. The loss is made good by water flowing from the soil into the roots, and thence within the xylem to the leaves. The factors that provide resistances to the flow of water from soil to root are set by the nature of the soil, the proliferation of roots within it, and the contact between the soil and the root. Root system architecture and the proliferation of lateral roots are covered in the following chapter, section 4.1.
Water removed by transpiration results in drier soil around roots compared with bulk soil. This provides the gradient in suction necessary for water flow towards roots to continue. As soil dries near the root surface, water flows radially from bulk soil to replenish it. When the bulk soil becomes drier, greater suctions are necessary to sustain the flow. The next section describes the capacity of different types of soils to hold water when wet, and release it to plants as they dry. It explains the terms field capacity and permanent wilting point. Following sections quantify the uptake of water by roots, and describe a major barrier to water uptake – the soil:root interface.
Water drains through soil due to gravity, leaving medium-sized pores still filled with water, and with thin films around soil particles. Soil is porous and holds water in its pores by capillary forces. As a soil dries, the larger pores drain and the remaining pores hold water ever more tenaciously. Water in these pores is under suction (negative hydrostatic pressure, P) and this suction typically ranges from about 10 kPa to about 1.5 MPa in soils supplying water to plants. At suctions of less than 10 kPa, water is held in such large pores that it is likely to drain quickly away; at suctions greater than 1.5 MPa, most plants are at their limit for exerting sufficient suction to extract the water.
When substantial rain falls on a freely draining soil, it may fill all the pores, even to the point of run-off. Thereafter, water quickly drains out of the largest pores under the influence of gravity into the drier soil below. This process of redistribution continues for days, even weeks, but it does so ever more slowly as the remaining largest pores continue to drain. During this time the hydraulic conductivity of the soil falls by several orders of magnitude because the resistance to viscous flow through water-filled pores depends inversely on the 4th power of their diameter.
After about 2 days of redistribution, the rate of drainage typically drops to only a few mm per day, which in the field is similar to other forms of water loss from the soil: uptake by roots, or evaporation from the soil surface. At this point there will be a suction (negative pressure) in the soil water of somewhere between 10 and 30 kPa, and the water content then is known as “field capacity” or “drained upper limit”.
Soil scientists classify soils according to particle size as:
| Gravel: | > 2 mm |
| Sand: | 0.05 – 2 mm |
| Silt: | 0.002 – 0.05 mm |
| Clay: | < 0.002 mm (2 µm) |
The structure and texture of the soil determines how much water can be held in it. Sand particles are large (50 mm - 2 mm) and hold onto little water, but a sandy soil provides good aeration. Sand holds little water because the pores between the grains are large. Therefore, its field capacity, the amount of water in the soil remaining a day or two after irrigation, can be as low as 10% (weight per volume; or 10 mL water per 100 mL soil volume).
Clay particles are much smaller (less than 2 mm) and easily compacted. That makes clay a good material for building bricks, but not so good for allowing water, air, and plant roots through. Clay particles have stacked platelets which provide large amounts of surface area. Clay soils store large amounts of water and have a field capacity above 40%, though much of that may be in pores too small for plants to extract water, as shown in the table below.
Silt is the medium size particle (2-50 mm), with better water retention than sand, but less nutrients than clay. Loam is a soil comprised of roughly equal amounts of sand and silt and a little less clay.
Different types of soil are comprised of various proportions of these particle sizes, as illustrated in Figure 3.37.

Figure 3.37 Textural classification of soils. Loam is a soil comprised of roughly equal amounts of sand and silt and a little less clay. http://imgkid.com/soil-texture-triangle.shtml
The diameter of pores in soil is roughly equal to one fifth of the diameter of the soil particles. Thus, at the boundaries between these classes, the approximate diameters of the pores would be as shown in Table 3.3 with the suction needed to drain them.
This table shows that many pores in a gravelly soil would drain at a suction of only about 1 kPa, but that a clay soil would need ten times this suction, close to 1 MPa, to drain many pores. Transpirational pull by plants can provide suctions above this, but there is a limit at which plants can maintain suction without the risk of embolism.
This term is used by crop physiologists, and often called the “lower limit of water extraction” by agronomists and crop modellers. When the water content of a soil is below the wilting point, plants have difficulty accessing it, as they cannot generate a sufficiently low water potential. In practice, this critical water potential has been found to be about -1.5 MPa, which effectively marks the lower limit of the available soil water.
Soil at wilting point is not dry. Different soil types hold very different amounts of moisture at their wilting points. As plant remove water and the soil starts to dry, the small pores make it difficult for roots to extract all the water, so clay soils hang onto their water more strongly than sandy or loamy soils, and results in the plant available water being less for clay soils than for loamy soils which have a lower clay content (Table 3.4). Silt contains pore sizes intermediate to clay and sand, and makes up about 50% of the composition of loamy soils (Figure 3.37) and give it the favourable property of retaining more water than sand as the soil but releasing it more easily than clay.
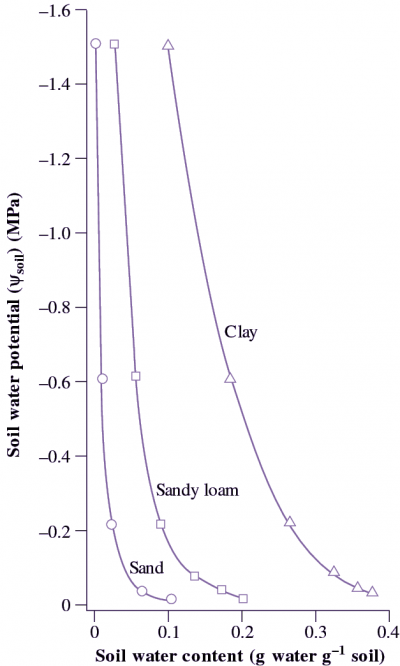
Figure 3.38 Clay soils are fine textured and have a greater water-holding capacity than do sandy soils that are composed of larger particles. Clay soils hold a greater amount of plant-available water between field capacity (Ψsoil about -0.02 MPa) and wilting point (Ψsoil about -1.5 MPa) than do sandy soils. In both situations, water is held with progressively stronger forces as the soil mass dries out. (R O. Slatyer and I.C McIlroy, 1961).
The relationship between soil water content and soil water potential (Ψsoil) is shown in Figure 3.38 for the three different soil types. Water is held with progressively stronger suctions as the soil dries, and at the permanent wilting point of -1.5 MPa clay soils retain much more water than sands or sandy loams that is not available to plants.
Another feature of clay soils that makes them less desirable for agriculture or horticulture is that root length density (length of roots per unit volume of soil) tends to be lower than in the lighter textured loamy and sandy soils. Despite their substantial moisture reserves, fine-textured clay soils are generally less hospitable to plant roots than loamy or sandy soils. As a result, plant-extractable moisture in clay soils is somewhat less than the soil’s physical properties alone would imply.
Field capacity is not a term relevant to pot experiments, unless they are very tall. After irrigation, a drained pot will contain much more water than soil in the field.
The soil at the bottom of a freshly watered and drained pot is inevitably saturated with water; if the pot is short the whole of the medium may have such little air-filled porosity that it becomes hypoxic. This is a special problem with field soils used in pots, for these typically do not contain many pores large enough to be drained at the small water suctions that prevail. Such suctions are zero at the bottom of a freshly drained pot and rise by 1 kPa for every 100 mm increment in height, leading to suctions at the top of a typical pot that are much less than the 10–30 kPa that occurs in soils in the field that have drained to ‘field capacity’ (Passioura 2006).
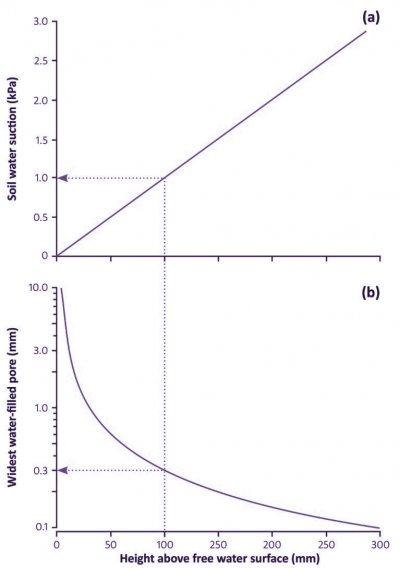
Figure 3.39 The relationships, at equilibrium, between soil water suction (a), effective diameter of largest water-filled pores (b), and height above a free water surface, such as a water table within the soil or the bottom of a recently drained pot. The dotted lines exemplify conditions at a height of 100 mm. (J.B. Passioura, Funct Plant Biol 33: 1075–1079, 2006)
When a pot has finished draining, the soil at the bottom is saturated: it has zero water suction. The suction varies linearly with height, as illustrated in Fig. 3.39, from zero at the bottom of the pot, to 10 H Pa, where H is the height of the pot in mm. Thus, a freshly watered and drained pot that is 100 mm high has a water suction at its top of 1 kPa, very much less than the 10–30 kPa that occurs in a freshly watered and drained soil in the field. Similarly, a pot that is 200 mm high has a suction of 2 kPa at the top. Thus the average suction and thence average soil water content of a freshly watered and drained pot depends on its height.
It is worth noting that the size and number of drainage holes in the bottom of the pot have no bearing on the distribution of suction with height at equilibrium. The rate at which equilibrium is attained will also depend little on the number and size of the drainage holes — just one hole of a few mm diameter is adequate.
The implication of these small suctions is that much larger pores contain water than in a drained soil in the field. For example, at the top of a pot that is 100mmhigh, and where the suction is 1 kPa, all pores less than 0.3 mm wide will contain water. This contrasts greatly with the field soil, in which the suction will be at least 10 kPa and the diameter of the largest water-filled pore will be 0.03 mm or even less.
This has considerable implications for doing pot experiments on the availability of soil water to plants using field soils. Standard watering techniques, which result in adding excess water that then drains from pots, lead to initial soil water contents that are much more than they would be in the freshly drained soil in the field. To match what happens in the field, it would be necessary to water the pots by weight to reproduce a water content consistent with a suction somewhere between 10 and 30 kPa. Further, the large initial water content can produce problems with aeration.
The plant nursery industry is well aware of the difficulties in adequately aerating pots. That is why their potting mixes contain peat or vermiculite or other bulky materials that create large pores of 1mm or more in diameter, which contain air at heights greater than 30mm above the bottom of a freshly drained pot. These large pores protect the roots from hypoxia in a material that might otherwise have a dangerously small air-filled porosity. Nevertheless, despite these large air-filled pores giving the roots growing in them access to oxygen, the interior of aggregates in the soil or potting mix will still be essentially saturated and possibly hypoxic.
Data for three different types of potting mix are shown in Figure 3.29: horticultural topsoil, commercial potting mix is designed for growing plants for sale in garden nurseries, and fine potting mix designed for growing Arabidopsis thaliana in small pots. The topsoil is the worst aerated, with the bottom 150mm of a freshly drained pot in danger of becoming hypoxic. It is notable that in the small pots (70 mm tall) often used for growing Arabidopsis, all of the medium is in danger of becoming hypoxic, for the porosity ranges from 0 to only 7%within the pot (Figure 3.40). With a frequent watering regime, say twice daily, the medium could be permanently hypoxic. Commercial potting mixes overcome this problem by using coarse materials in the mix, which create many large pores (>1 mm diameter) that drain at small suctions.
Field capacity should therefore not be confused with the water content of a drained pot, which should be called “pot capacity”.
Flow of water through soil is induced by gradients in hydrostatic pressure, P. The rate of flow, F (m s–1), depends on both the gradient in P and on hydraulic conductivity, K (m2 MPa–1 s–1), of the soil:
\[F=K \frac{dP}{dx} \tag{8}\]
where x (m) is distance. This equation is Darcy’s Law. Conductivity, K, varies enormously, by about a thousand-fold, over the range of available water content. The reason for this large range is that water flows much more easily in a large pore than in a small one. As explained earlier (Section 3.1), the flow rate varies according to Poiseuille’s Law — the flow in capillary tubes depends on the fourth power of the diameter. As the soil dries, the large pores are empty and water is drawn from smaller and smaller pores.
Water removed by transpiration results in drier soil around roots compared with bulk soil. As soil dries near the root surface, water flows radially from bulk soil to replenish it. Calculated distributions of water content and pore water pressure with radial distance from an absorbing root predict a pronounced increase in suction adjacent to the root.
Roots are cylindrical, so the flow of water to them is radial. This has considerable consequences: the flow lines converge as they approach the root, which requires increasing gradients of pressure in the soil water to keep the water flowing (Figure 3.41).
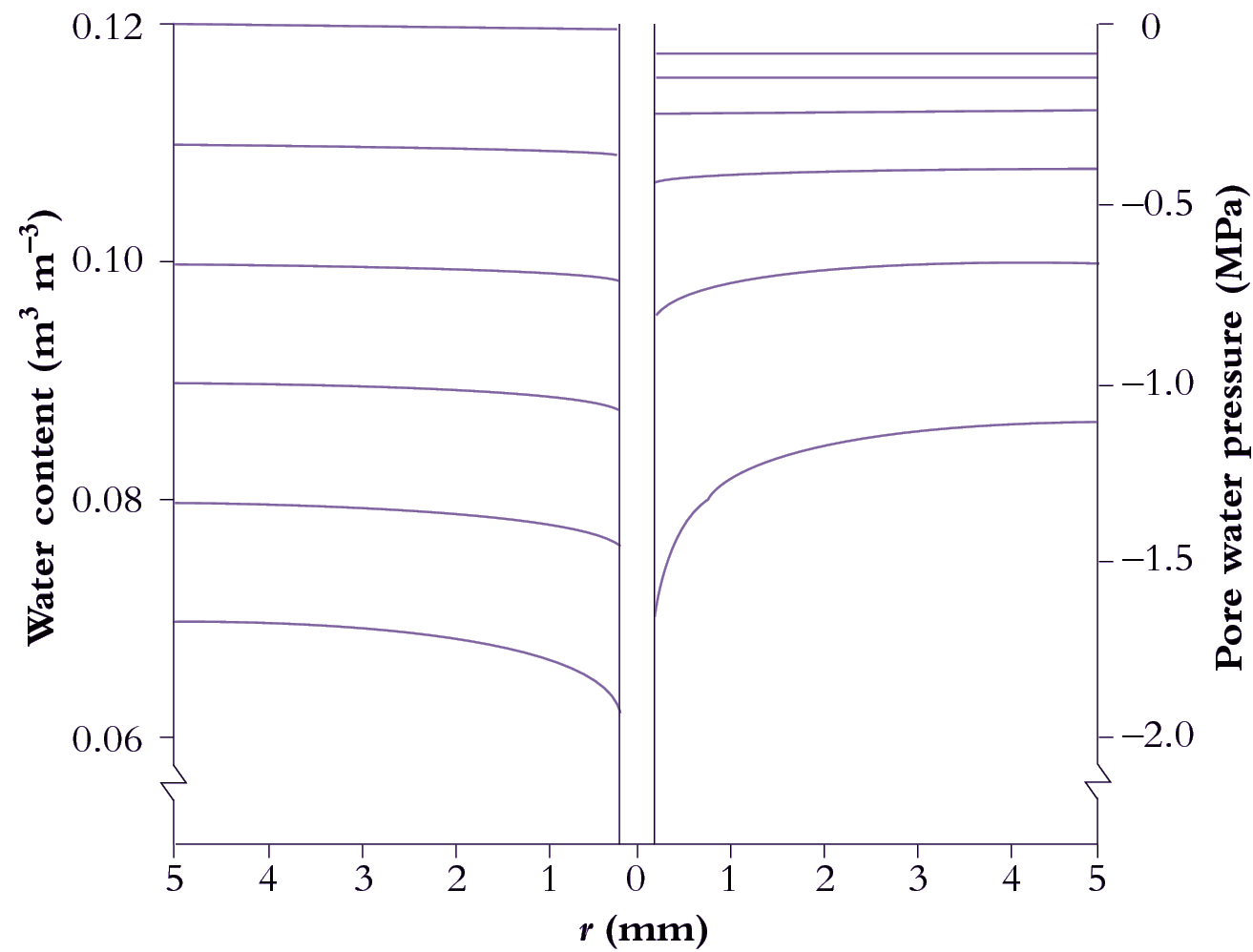
Figure 3.41 Calculated distributions of volumetric soil water content (left) and pressure in water-filled pores (right) as functions of distance from a model root. Pressures become more negative over time, indicating increasing suction. Horizontal lines denote water status on each of six successive days (day 1 is uppermost). The steepening of curves at later times reflects how transport of water from bulk soil to the root surface becomes increasingly difficult as the soil dries. r = distance from central axis of root.
A radial flow of water from the bulk soil towards roots of transpiring plants is generated by suction at the root surface. However, because K decreases with falling water content, there is a limit to how fast roots can extract water from soil. Once this limit has been reached, increasing suction by roots simply steepens the gradient in P to match the fall in K close to root surfaces so that the product of the two (Equation 3.1) remains the same.
Although soil water is driven by gradients of pressure, it is necessary when water content is changing to describe this flow in terms of gradients in volumetric water content, θ (m3 m–3). The coefficient relating flow rate to the gradient in water content is known as diffusivity, D (m2 s–1), and the appropriate equation is formally analogous to Fick’s First Law of diffusion:
\[F=D \frac{d\theta}{dx} \tag{9}\]
This equation can be elaborated to allow for the cylindrical flow, and then solved to derive an approximate relationship for the uptake of water by a population of roots:
\[Q \approx 2D*\Delta \theta * L \tag{10}\]
where Q is the flow rate of water through the soil, (m3 m–3 s–1), now expressed as the overall rate of change of θ in the sample soil, and L is the rooting density, average length of absorbing root per unit volume of soil (m m–3).
Like K, D varies with the soil water content, although not so widely. Laboratory measurements of D, which are so far the only ones that have been made with some accuracy, show that D is about 10-7 m2s-1 when the soil is fairly wet, and falls to about 10-9 m2s-1 once the soil has dried far enough for the soil water suction to exceed about 300 kPa. Where D is of the order of 10-9 m2 s-1 one can calculate from eqn 3.3 that wherever the density of roots exceeds about 1 cm per cm3 of soil (104 m m-3) the flow of water through the soil is not likely to limit uptake until there is almost no available water left in the soil. But where there is less than about 1 mm of root per cm3 (103 m m-3) of soil, uptake is likely to be sufficiently limited by flow through the soil that it would take several days for the roots to extract most of the available water.
Many experiments have been done to explore this theory, with mixed results. Most have involved growing plants in repacked soil in controlled laboratory conditions. Some have confirmed the theory, many have not. The most likely reasons for the discrepancies is that interfacial effects - at the junction between the surface of the root and the soil - come into play. These are discussed in the next section.
In field soil, the concentration of roots in the topsoil is usually so high that the local rate of uptake of water is unlikely to be ever limited by the properties of the soil. It is in the subsoil that the rooting density drops to a level at which flow through the soil may limit the rate of uptake. Further, the rate of uptake is often much lower than what the simple theory would predict, even when the often sparse rooting density is taking into account.
In subsoil, there are other possible reason for the discrepancy between theory and observation. One is that, in contrast to disturbed soil, either in ploughed topsoil or repacked in lab experiments, roots in the subsoil do not ramify more or less randomly through the soil. Subsoils are usually dense and difficult to penetrate. Roots grow predominantly in pre-existing fissures or in continuous large pores, biopores, made by previous roots or soil fauna (Figure 3.42).
A second reason is that it may be wrong to extrapolate laboratory measurements of D in repacked soil to undisturbed soil in the field. The undisturbed structure of the soil may inhibit the flow of water. For example, the formation of aggregates of particles in the soil often results in particles of clay (which are usually in the form of small plates) becoming oriented parallel to the surface. Such orientation is likely to increase greatly the flow path for the water, but so far no reliable measurements of D have been yet made on undisturbed subsoil.
In summary, the dense root systems common in topsoils extract water effectively from surface soil layers. Extracting water from subsoil layers is more difficult. Australian subsoils are typically inhospitable to roots. They are dense, have a large resistance to penetration. They are often sodic, that is, sodium dominates the exchange complexes on soil particles, altering the soil structure so that it sets like concrete when dry, and becomes impermeable to water when wet. Moreover, subsoils can be acutely deficient in some nutrients that are required locally by roots. Native vegetation overcomes these difficulties by forming deep biopores in the subsoil. For example, roots of jarrah trees can create and maintain a path to water deep in the subsoil, possibly even as far as a water table 20 m below the surface.
The junction between root and soil is more than just two surfaces touching. It is often marked by a mucilaginous layer, rich in bacteria and fungi, that may be a few hundred micrometres thick, and in which adjacent soil particles are half or even wholly embedded. This is called the rhizosphere (Chapter 4). The hydraulic conductivity of this layer is not known, but there are two properties of this interfacial zone that may influence the flow of water across it. The first is that extensive gaps may occur within it, which strongly impede the flow. The second is that any exclusion of ions from the soil solution may result in large increases in the concentrations of these ions at the surface of the roots and this, because of the osmotic effects, would also impede the flow of water.
Water usually flows from soil to root as liquid, carrying with it dissolved nutrients. But there may be times when the hydraulic continuity between root and soil is so poor that a substantial proportion of the flow of water is as vapour. So far, nobody has managed to measure such flows, or even the relative importance of liquid and vapour flow, but their possible importance can be appreciated with the help of a few calculations.
The flow of vapour through soil is by diffusion, in contrast to that of liquid water, which moves in bulk. The consequence of this, and the fact that the vapour pressure of water is close to saturated in moist soil so that gradients in it are slight, is that water flows as vapour many times more slowly, in response to a given difference in water potential, than it does as liquid.
There are two main reasons why a root may be in poor hydraulic contact with the soil. The first is that it may be growing in a pre-existing pore larger than itself, so that it makes only glancing contact with the wall of the pore (see Figure 3.42 above). The second is that it has shrunk within a pore that it had itself made and which it had previously fitted snugly. What would induce a root to shrink? A fall in the water potential of the cortex would do so, for the cells there are thin-walled and separated in part by intercellular gas spaces, so they are likely to buckle. Observations made in rhizotrons (glass-walled tunnels for observing the behaviour of roots in the field) clearly show a diurnal shrinkage in cotton roots of up to 40% where the roots are growing in large pores, but we still do not know, because they are so difficult to observe, whether roots growing in intimate contact with the soil are similarly prone to shrink. A few observations made using neutron autoradiography have shown no shrinkage in roots growing in the field.
Because of the small size of the interfacial zone, it is very difficult to measure concentrations of ions within it. Rough estimates have been made by carefully separating the roots from the bulk of the soil, leaving only tenacious soil attached, then shaking off this remaining soil and analysing it. Such analyses do show somewhat higher concentrations (compared with those in the bulk soil) of ions such as sodium that we would expect to be largely excluded by the roots. But because the gradients in concentration are likely to be very large close to the root, these analyses are hard to assess for their consequences on the water relations of the plant. The gradients are likely to be especially large when the soil is becoming fairly dry, for the diffusion coefficient for the solutes falls by a few orders of magnitude as the soil dries, so that any excluded solutes will diffuse away from the root surface only very slowly.