Figure 3.61. Guard cells are structured so that high turgor pressure opens the stomatal pore, and low turgor pressure closes the pore. Left (Lower image), Partially open Tradescantia virginiana stoma with 0.2 MPa guard cell turgor, as measured directly with a guard cell pressure probe (shown). Right (upper image) same stoma showing the aperture almost fully open, with 3.6 MPa guard cell turgor. (Images and data courtesy P. Franks).
Water uptake by cells is driven by solute uptake. Osmotically-driven water uptake generates the turgor pressure needed for maintenance of cell volume, and for specific cell functions that depend on controlled changes in turgor. The rapid influxes or effluxes of water that cause rapid changes in cell volume in key cells are brought about by ion influxes or effluxes.
Rapid changes in turgor cause the swelling or shrinking of guard cells in leaves that controls the opening and closing of stomata. The cell walls of guard cells are structured so that high turgor pressure pushes them apart and opens the stomatal pore. Low turgor pressure allows them to collapse and close the pore (Figure 3.61). Influxes or effluxes of K+ along with accompanying anions causes the osmotically-driven water uptake or loss
Whole leaves or parts of leaves can move quickly. Changes in the turgor of a group of cells at the base of leaves, the pulvinus, cause leaves to fold quickly in response to touch, as in the ‘sensitive plant’ Mimosa pudica, (Figure 3.62)
Figure 3.62. Seismonastic movement of pinnae and pinnules in leaves of the sensitive plant (Mimosa sensitiva) (a) before and after touch stimulation. (Photographs courtesy J.H. Palmer)
Turgor changes also change the curvature of hairs of insectivorous plants. In the case of the Venus fly trap, sensory hairs coupled to an electrical signalling system require stimulation at least twice within a 30 s period (Simons 1992). This appears to allow the plant to discriminate single pieces of debris from an insect crawling within the trap. Most seismonastic movements result from the explosive loss of water from turgid ‘motor’ cells, causing the cells temporarily to collapse and inducing very quick curvature in the organ where they are located.
Similar mechanism causes the slower folding of leaves at night into special positions to reduce heat loss, as in the prayer plant. This also occurs in many legumes. Charles Darwin measured the folding of leaves at nightfall in white clover, and wrote: “The two lateral leaflets will be seen in the evening to twist and approach each other, until their surfaces come into contact, and they bend downwards. This requires a considerable amount of torsion in the pulvinus. The terminal leaflet merely rises up without any twisting and bends over until it forms a roof” (Figure 3.63).
Figure 3.63 The nictitropic movements of leaves of white clover (Trifolium repens) from daytime (A) to ‘sleeping’ position (B). (Charles Darwin, The Power of Movement in Plants, 1881). (Diagram courtesy R. Purdie)
Movement of some plant organs can be staggeringly fast. The firing of the reproductive structure (“column”) of trigger plants (Stylidium genus) in response to the landing of a pollinating insect may take only 15 msec (Figure 3.64).
Figure 3.64 Sequence of superimposed images captures the flower column of a trigger plant (Stylidium crassifolium) as it ‘fires’ in response to a physical stimulus (insect landing, seen on upper right). The column rotates through 200° from a ‘cocked position’ to a relaxed position in 20 ms (photographs taken at 2 ms intervals). (Findlay and Findlay 1975)
The kinetic energy manifested in this rapid firing is derived from events controlled at a membrane level. Ions transported into specialised cells cause hydrostatic (turgor) pressure to develop which is suddenly dissipated following mechanical stimulation
Water transport into a cell anywhere in the plant is governed by solute uptake which in turn is governed by the permeability of membranes to water as well as solutes.
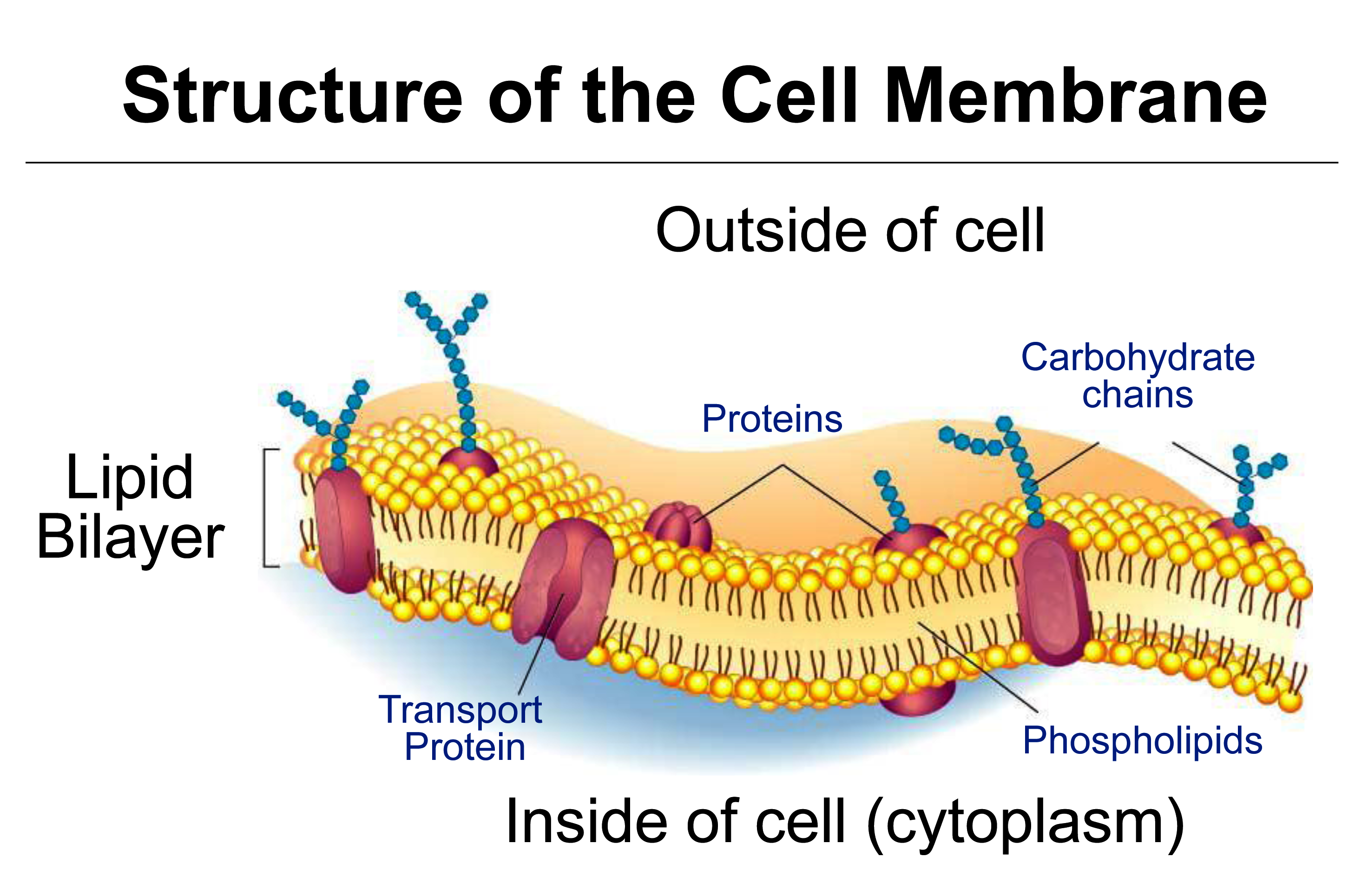
This section covers diffusion of molecules, and permeability of cell membranes, essential to the process of osmosis. Cell membranes are bilayers of phospholipids in which transport proteins are embedded (Figure 3.65).
Figure 3.65 Diagram of a cell membrane with transport proteins embedded in the phospholiped bilayers. (Image courtesy M. Hrmova)
A plant membrane is often described as semi-permeable, meaning permeable to water but not biological solutes. However the membrane is not 100% permeable to water, as water can enter cells only by being transported through aquaporins, neither is it 100% impermeable to solutes, as solutes can slowly permeate the membrane particularly through specific transport proteins.
Unrestricted movement of water relative to solutes is the basis of osmosis, and in plants the generation of turgor pressure, \(P\). The principles of diffusion and selectivity, which are used to describe differential rates of molecular movement, provide a physical rationale for osmosis.
In a homogeneous medium, net movement of molecules down their concentration gradient is described by Fick’s First Law of diffusion. The molecule and medium may be a solute in water, a gas in air or a molecule within the lipid bilayer. Fick’s Law holds when the medium is homogeneous in all respects except for the concentration of the molecule. If there was an electric field or a pressure gradient then Fick’s Law may not apply. Considering the case of a solute in water, say, sugar, Fick’s Law states that net movement of this solute, also called the net flux \(J_s\), is proportional to the concentration gradient of the solute \( \Delta C_s / \Delta x \):
\[ J_s = -D_s \frac{\Delta C_s}{\Delta x} \tag{12}\]
The diffusion coefficient (\(D_s\)) is a constant of proportionality between flux, \(J_s\), and concentration gradient (mol m-4), where solute concentration (\(C_s\), mol m-3) varies over a distance (\( \Delta x\), m). Flux is measured as moles of solute crossing a unit area per unit time (mol m–2 s–1), so \(D_s\) has the units m2 s–1. \(D_s\) has a unique value for a particular solute in water which would be quite different from \(D_s\) for the same solute in another medium, for example the oily interior of a lipid membrane.
Across a membrane, the movement of a molecule from one solution to another can be described by Fick’s Law applied to each phase (solution 1–membrane–solution 2). However, flux across the membrane also depends on the ability of the molecule to cross boundaries (i.e. to partition) from solution into the hydrophobic membrane and then from the membrane back into solution. Another difficulty is that the thickness of membranes is relatively undefined and we need to know this for Fick’s equation above (\( \Delta x \)). The two solutions might differ in pressure and voltage and these can change steeply across a membrane; however, if for simplicity we consider a neutral solute at low concentration, these factors are not relevant (see below for charged molecules). A practical quantitative description of the flux of neutral molecules across membranes uses an expression intuitively related to Fick’s Law stating that flux across a membrane (\( J_s \)) of a neutral molecule is proportional to the difference in concentration \(\Delta C_s\):
\[ J_s = P_s \Delta C_s \tag{13}\]
Figure 3.66. The range of permeability coefficients for various ions, solutes and water in plant membranes (vertical bars) and artificial phospholipids (arrows). Note that the permeability of ions as they cross plant membranes is higher than through the artificial lipid bilayer.
The constant of proportionality in this case is the permeability coefficient (\( P_s \)), expressed in m s–1. When \( P_s \) is large, solutes will diffuse rapidly across a membrane under a given concentration gradient. \( P_s \) embodies several factors: partitioning between solution and membrane, membrane thickness and diffusion coefficient of the solute in the membrane which may be largely depend on specific transporters. It can be used to compare different membranes and to compare treatments that might alter the ability of a solute to move across the membrane.
Note that Equation 13 assumes that the concentration gradient is only across the membrane, and that when the permeability coefficient is measured, concentration gradients leading to diffusion in solutions adjacent to the membrane will not be significant. If the two solutions are stirred rapidly then this will help to justify this assumption. However, there is always an unstirred layer adjacent to the membrane through which diffusion occurs, and for molecules that can permeate the membrane very rapidly the unstirred layer can be a problem for the correct measurement of permeability.
Solute movement across membranes can be across the lipid phase of the membrance, depending on size, charge and polarity, and it can be assisted by transport proteins embedded in the membrane.
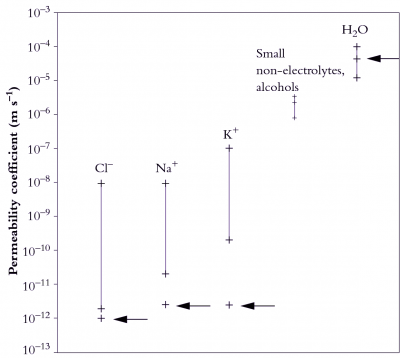
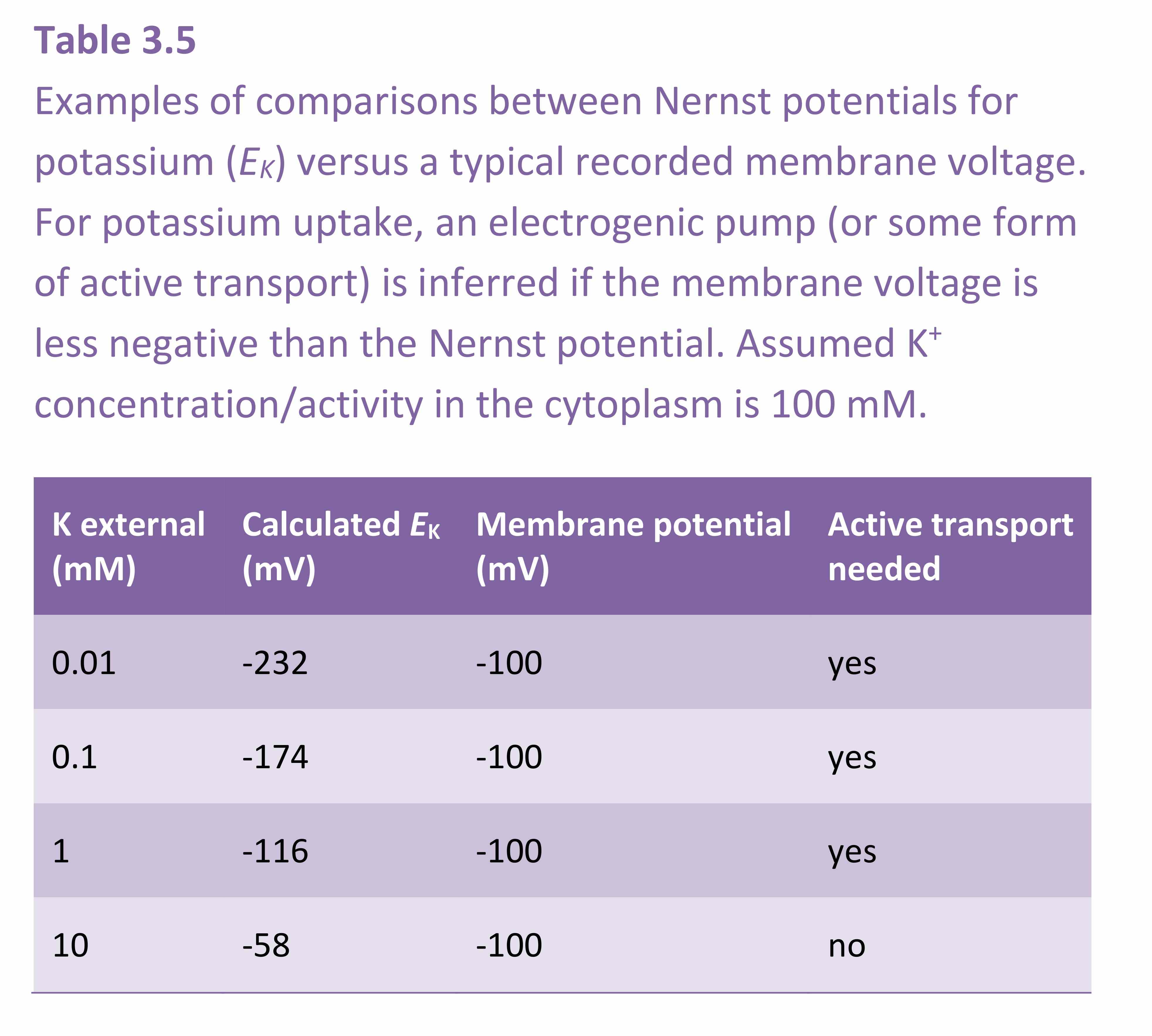
The range of permeability coefficients for various ions, solutes and water in plant membranes is shown in Figure 3.66, along with the permeability of artificial phospholipid bilayers. The permeability of ions as they cross membranes is higher than that through the artificial lipid bilayer, especially for potassium, indicating the presence of specialised permeation mechanisms, ion transporters, in plant membranes. Water permeabilities are high in both plant and artificial membranes but can range over an order of magnitude in plant membranes. This variability may be partially accounted for by the activity of aquaporins.
A comparison of artificial lipid membranes with biological membranes supports this notion because it shows that many molecules and ions permeate biological membranes much faster than would be predicted on the basis of oil solubility and size (Figure 3.66). For these solutes there are transport proteins in biological membranes that increase solute permeability.
Plant membranes are ideally semipermeable, that is, water permeability is much larger than solute permeability.
The degree of semi-permeability that a membrane shows for a particular solute is measured as the reflection coefficient, \( \sigma \):
\[ \sigma = 1 - \frac{\text{Solute Permeability}}{\text{Water Permeability}} \tag{15}\]
Figure 3.67. Turgor pressure (\( P \)) in a Tradescantia virginiana epidermal cell as a function of time after the external osmotic pressure was changed with different test solutes. Measurements were made with a pressure probe. (Tyerman and Steudle 1982)
If a plant cell or an epidermal strip is bathed in solution, the reflection coefficient for a particular solute can also be considered as the ratio of the effective osmotic pressure versus the actual osmotic pressure in the bathing solution.
The reflection coefficient usually ranges between zero and one, being zero for molecules with properties similar to water, like methanol, to one for large non-polar molecules like sucrose.
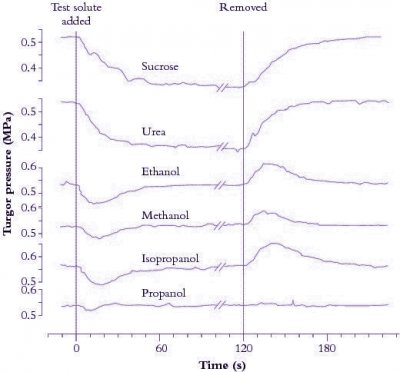
Figure 3.67 shows turgor pressure (\( P \)) in a Tradescantia virginiana epidermal cell as a function of time after the external osmotic pressure was changed with different test solutes. The initial decrease in \( P \) is due to water flow out of the cell and is larger for solutes with a reflection coefficient near one (sucrose and urea). Propanol induces no drop in \( P \), indicating that its reflection coefficient is zero. Subsequent increase in \( P \) is due to penetration of particular solutes such as alcohol across the cell membrane. Water flows osmotically with the solute thereby increasing \( P \) to its original value. Removing solutes reverses osmotic effects. That is, a decrease in \( P \) follows the initial inflow of water as solutes (e.g. alcohols) diffuse out of cells.
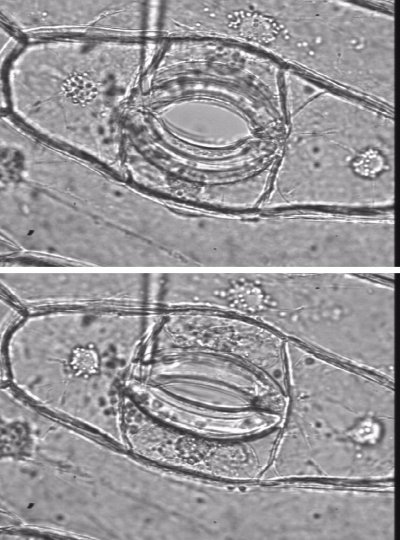
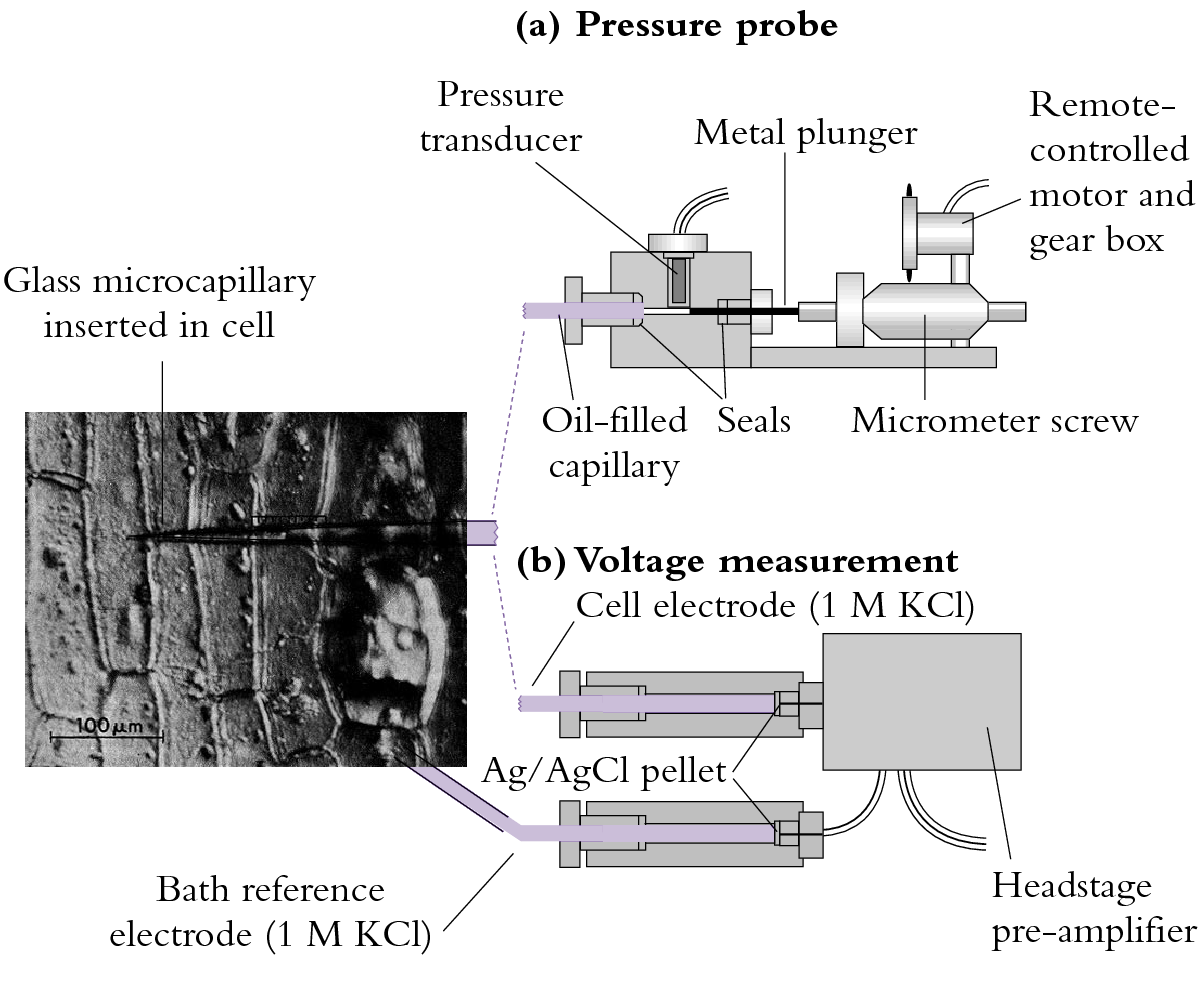
The pressure probe apparatus is illustrated in Figure 3.68(a).
Figure 3.68 (a) A miniaturised pressure probe. An oil-filled capillary of about 1 µm diameter is inserted into a cell whose turgor pressure (\( P \)) is transmitted through the oil to a miniature pressure transducer. The voltage output of the transducer is proportional to \( P \). A metal plunger acting as a piston can be used via remote control to vary cell \( P \).
Using the pressure probe to measure turgor pressure, \( P \), the membrane is found to be ideally semipermeable for sucrose (\( \sigma = 1 \)); that is, the membrane almost totally ‘reflects’ sucrose. Over long periods, sucrose is taken up slowly but permeability relative to water is negligible. In this case, the change in \( P \) would be equivalent to the change in \( \pi \). If \( \sigma \) is near zero, then water and the solute (say, propanol) are equivalent in terms of permeability. No change in \( P \) can be generated across a cell wall if \( \sigma \) is zero.
Diffusion of neutral molecules at low concentrations is driven by differences in concentrations across membranes, as explained above. There are other forces that may influence solute diffusion, including the voltage gradient when considering movement of charged molecules (ions) and the hydrostatic pressure when considering movement of highly concentrated molecules (such as water in solutions). These forces can be added to give the total potential energy of a particular molecule (\( \mu_s \)) relative to a reference value (\( \mu_s^* \)):
\[ \mu_s = \mu_s^* + RT\ln C_s + z_s FE + V_sP \tag{16}\]
Gravitational potential energy could also be added to this equation if we were to examine the total potential over a substantial height difference, but for movement of molecules across membranes this is not relevant.
The concentration term (\( RT\ln C_s \)) is a measure of the effect on chemical potential of the concentration of solutes (actually the activity of the solutes which is usually somewhat less than total concentration). The gas constant, \(R\) (8.314 joules mol–1K–1), and absolute temperature, \(T\) (in degrees Kelvin, which is equals 273 plus temperature in degrees Celsius), account for the effects of temperature on chemical potential.
Incidentally, from this term the well-known van‘t Hoff relation is derived for osmotic pressure \(\pi\), as given at the beginning of this chapter:
\[ \pi = RTC \tag{1} \]
Figure 3.69. Illustration of how electrical and concentration terms contribute to electrochemical potential of ions. Calcium (top) commonly tends to leak into cells and must be pumped out whereas chloride tends to leak out and must be pumped in to be accumulated.
where \(R\) is the gas constant (8.31 joules mol–1K–1), \(T\) is the absolute temperature in degrees Kelvin (273 plus degrees Celsius), and \( C \) is the solute concentration (Osmoles L-1). At 25 ºC, \(RT\) equals 2.48 liter-MPa per mole, and (\( \pi \)) is in units of MPa. Hence a concentration of 200 mOsmoles L-1 has an osmotic pressure of 0.5 MPa.
The electrical term (\( z_s FE \) ) is a measure of the effect of voltage (\( E \) ) on chemical potential. The charge on a solute (\( z \)) determines whether an ion is repelled or attracted by a particular voltage. Electrical charge and concentration are related by the Faraday constant (\( F\) ) which is 96,490 coulombs mol–1. The electrical and concentration terms form the basis of the Nernst equation (see below).
The pressure term measures the effect of hydrostatic pressure on chemical potential, where \(P = \text{Pressure}\) and \( \overline{V}_s \) is the partial molar volume of the solute.
Molecules diffuse across a membrane down a chemical potential gradient, that is, from higher to lower chemical potential. Diffusion continues until the difference in chemical potential equals zero, when equilibrium is reached. The direction of a chemical potential gradient relative to transport of a molecule across that membrane is important because it indicates whether energy is or is not added to make transport proceed (Figure 3.69). Osmotic ‘engines’ must actively pump solutes against a chemical potential gradient across membranes to generate \(P\) in a cell. Sometimes ions move against a concentration gradient even when the flux is entirely passive (no energy input) because the voltage term dominates the concentration term in Equation 16. In this case, ions flow according to gradients in electrical and total chemical potential. For this reason, the chemical potential of ions is best referred to as the electrochemical potential.
Ions such as potassium and chloride (K+ and Cl–) are major osmotic solutes in plant cells. Deficiency of either of these two nutrients can increase a plant’s susceptibility to wilting. Most other inorganic nutrients are acquired as ions and some major organic metabolites involved in photosynthesis and nitrogen fixation bear a charge at physiological pH. For example, malic acid is a four-carbon organic acid that dissociates to the divalent malate anion at neutral pH. Calcium (Ca2+) fluxes across cell membranes are involved in cell signalling and although not osmotically significant they play a crucial role in the way cells communicate and self-regulate. Finally, some ions are used to store energy but need not occur at osmotically significant concentrations. Cell membranes from all kingdoms use hydrogen (H+) ions (protons) in one way or another to store energy that can be used to move other ions or to manufacture ATP (Chapter 2). The highest concentration of H+ that occurs is only a few millimoles per litre yet H+ plays a central role in energy metabolism.
To understand ion movement across membranes, two crucial points must be understood: (1) ionic fluxes alter and at the same time are determined by voltage across the membrane; (2) in all solutions bounded by cell membranes, the number of negative charges is balanced by the number of positive charges. Membrane potential is attributable to a minute amount of charge imbalance that occurs on membrane surfaces. So at constant membrane potential the flux of positive ions across a membrane must balance the flux of negative ions. Most biological membranes have a capacitance of about 1 microFarad cm–2 which means that to alter membrane voltage by 0.1 V, the membrane need only acquire or lose about 1 pmol of univalent ion cm–2 of membrane. A univalent ion is one with a single positive (e.g. K+) or negative (e.g. Cl–) atomic charge. In a plant cell of about 650 pL, this represents a change in charge averaged over the entire cell volume of 12 nmol L–1!
The membrane voltage or membrane potential difference, as it is sometimes called, can be measured by inserting a fine capillary electrode into a plant cell (Figure 3.68b). Membrane voltage is measured with respect to solution bathing the cell and in most plant cells the voltage is negative across the plasma membrane. That is, the cytoplasm has a charge of –0.1 to –0.3 V (–100 to –300 mV) at steady state with occasional transients that may give the membrane a positive voltage. The tonoplast membrane that surrounds the central vacuole is generally 20 to 40 mV more positive than the cytoplasm (still negative with respect to the outside medium).
Figure 3.68. (a) Techniques employing fine glass capillaries to probe plant cells. (b) A probe for measuring membrane voltage. The capillary is filled with 1 mol L-1 KCl and connected to a silver/silver chloride electrode that acts as an interface between solution voltage and input to the amplifier. A voltage is always measured with respect to a reference (in this case, a bath electrode). The headstage amplifier is close to the electrodes to minimise noise.
Cell membrane voltages can be affected by ion pumps, diffusion potential and fixed charges on either side of the membrane.
Special mention needs to be made of one such fixed charge which arises from galacturonic acid residues in cell walls. Although cations move to neutralise this fixed negative change, there is still a net negative potential associated with cell walls (Donnan potential). In spite of being external to the plasma membrane, the Donnan potential is in series with it and probably adds to what we measure as the membrane potential with electrodes.
Most charge on macromolecules in the cytoplasm is also negative (e.g. nucleic acids, proteins) and because of their size it can be regarded as a fixed negative charge. This has consequences on the water relations of the cytoplasm in that they exert a significant osmotic potential, even though not in solution, as do the clay particles in soil (Passioura 1980).
Different ions have different permeabilities in membranes. Potassium, for example, is usually the most permeable ion, entering under most conditions about 10 to 100 times faster than Cl– Since ions diffuse at different rates across membranes, a slight charge imbalance occurs and gives rise to a membrane voltage (Figure 3.69). This voltage in turn slows down movement of the rapidly moving ion so that the counter-ion catches up. The result is that when net charge balance is achieved, a diffusion potential has developed that is a function of the permeabilities (\( P_\text{ion} \)) of all diffusible ions present and concentrations of each ion in each compartment.
Figure 3.70. How a diffusion potential develops through differential movement of an ion across a membrane that is permeable to K+ but not Cl-. The left hand compartment (representing the cytoplasm) has the higher concentration of K+ and Cl-, as indicated by the size of the letters. The right hand compartment represents the apoplast (cell wall). Initially (a), a minute amount of K+ crosses the membrane along its concentration gradient, and creates a positive charge in the right-hand compartment as K+ concentration there rises above Cl- concentration. At equilibrium (b), a diffusion potential is established, and further movement of K+ is prevented. Concentrations never equalise on both sides because K+ is the only species able to move through the membrane.
The Goldman equation describes this phenomenon and gives the membrane voltage (\( \Delta E \) ) that would develop due to diffusion of ions. The Goldman equation for the ions that mostly determine this diffusion potential (K+, Na+ and Cl–) is given by:
\[ \Delta E = \frac{RT}{F} \ln \frac{P^{}_K C_K^o + P^{}_{Na}C_{Na}^o + P^{}_{Cl}C_{Cl}^i}{P^{}_K C_K^i + P^{}_{Na}C_{Na}^i + P^{}_{Cl}C_{Cl}^o} \tag{17}\]
The superscripts refer to the inside (i) or outside (o) of the membrane and \( R \), \( T \), \( F \) and \( C \) are defined elsewhere (Equation 4.5). Note that the concentration terms for Cl– are reversed in the numerator and denominator compared to the cations. This is because Cl– is the only anion represented. Many texts do not include H+ in the Goldman equation because, in spite of high permeability of H+, diffusion of H+ is unlikely to have a strong effect on ΔE at such low (micromolar) concentrations. However, membrane potential is occasionally dominated by the diffusion of H+, indicating that H+ permeability must be exceedingly high. For example, local variations in pH cause alkaline bands to form on Chara corallina cells and in the leaves of aquatic plants at high pH.
When one ion has a very high permeability compared to all other ions in the system the membrane will behave as an ion-sensitive electrode for that ion (e.g. Figure 4.7). A pH electrode which is sensitive to H+ flux across a glass membrane serves as an analogy. In the case of a single ion, the Goldman equation can be reduced to the simpler Nernst equation that yields the equilibrium membrane potential which would develop for a particular concentration gradient across a membrane.
\[ \Delta E = \frac{RT}{zF} \ln \frac{C_o}{C_i} \tag{18}\]
where \( R \) and \( T \) are the gas constant and temperature (degrees Kelvin) and \( F \) is the Faraday constant. Typical charges on ions (\( z \)) would be –1 for Cl-, +1 for K+) and so on. This term in the Nernst equation gives the correct sign for the calculated membrane potential.
The Nernst equation is routinely used by electro-physiologists to calculate the equilibrium potential for each ion. Theoretical equilibrium potentials can then be compared with the actual membrane potential in order to decide whether the membrane is highly permeable to one particular ion. For example, in many plant cells there are K+ channels that open under particular circumstances. When this occurs, the membrane becomes highly permeable to K+ and the measured membrane potential very nearly equals the Nernst potential for K+. The Nernst equation can also be used as a guide in deciding whether there is active transport through a membrane. For example, when the measured membrane potential is less negative than the most negative Nernst potential, an electrogenic pump must be engaged for K+ to enter the cell (Table 4.1). If the membrane potential is less negative than the Nernst potential and if a K+ channel were open then K+ would leak out of the cell. For K+ uptake to occur with such a gradient for passive efflux then energy would need to be generated.
Equation 4.7 can be rewritten with constants solved and log10 substituted for the natural logarithm. This yields a useful form as follows,
\[ \Delta E = \frac{58}{z} \log_{10} \frac{C_o}{C_i} \tag{19} \]
showing that 10-fold differences in concentration across a membrane are maintained by a 58 mV charge separation for monovalent ions. For example, -58 mV will keep K+ concentrations 10 times higher inside a cell than in the external medium and Cl– concentrations 10 times lower. Plasma membranes are normally about -116 mV, which would keep K+ concentrations inside a cell 100 times higher and Cl- concentrations 100 times lower than in the external solution.
Internal membranes have a different electrical potential, the mitochondria being more negative than the plasma membrane (around -180 mV) and the chloroplast and tonoplast being slightly positive (around +50 mV).
The concentration of an ion inside a cell membrane (\( C_i \)) that would occur at equilibrium for any \( C_o \) and \( \Delta E \) can be calculated by rearranging the above equation as:
\[ \log_{10} C_i = \log_{10} C_o - \frac{z\Delta E}{58} \tag{20} \]
remembering that \( z \) and \( \Delta E \) can be positive or negative, depending on the ion and the particular cell membrane being considered.
Plant and animal membranes have much higher permeability to water than can be explained by diffusion rates through a lipid bilayer. Furthermore, the activation energy for diffusion of water across a plant membrane is lower than would be expected across a lipid bilayer, where water has to overcome the high-energy barrier of partitioning into a very hydrophobic oily layer. Some reports put the activation energy for water flow across membranes as low as the value for free diffusion of water. In other words, water enters the membrane about as readily as it diffuses through a solution. This suggests that water is moving across the membrane through a pathway other than the lipid, perhaps some kind of water pore or water channel. Since the discovery of water channel proteins in animal cell membranes, molecular biologists discovered that similar proteins exist in plants.
Water channels, like ion channels, are proteins embedded in membranes that facilitate the passive transport (non-energised flow) of water or ions down their respective energy gradients. Movement of a solute or water through these transport proteins is not coupled to movement of any other solute, and does not require ATP. The proteins that facilitate passive transport are diverse; some are specific for particular ions and allow high transport rates per protein molecule (ion channels), some are specific for water (water channels or aquaporins) and some are specific for neutral solutes and may have slower transport rates per protein molecule.
Why are there water channels in membranes when the lipid itself is already somewhat permeable to water? There are several rationales for the presence of water channels in plant membranes. One is that specialised transport proteins can control water flow. That is, a water channel protein may be turned on and off, for example by phosphorylation, while water permeability of the lipid is essentially constant. In animal cells, such as in the kidney, water channels are controlled by antidiuretic hormones. Plant hormones could also influence the function of water channels. A second rationale for the presence of water channnels is to balance water flow and prevent bottlenecks. In the root, water channels are most abundent in the endodermis and inner stele where water flow across membranes is rapid.
The approach to studying water channels has been to inject genetic material from plants into Xenopus oocytes (a particular type of frog’s egg). The Xenopus oocyte is particularly useful because it is large, enabling observations of cell response to foreign proteins. It is one of several expression systems along with Chara (giant algal cells) and yeast cells. cDNA arising from screens of cDNA libraries can be injected into the Xenopus nucleus, or poly (A)+-RNA can be injected into the oocyte cytoplasm where it is translated. Plant water transport proteins expressed in the oocyte plasma membrane result in physiological changes; for example, the oocyte swells rapidly when the external osmotic pressure in the bathing medium is lowered (Figure 3.71a). The first plant aquaporin gTIP (Tonoplast Integral Protein) that was discovered occurs in the tonoplast and probably accounts for its high water permeability. Provided that the increase in water permeability is not a consequence of some other change or a side effect of other types of transport, it can be concluded that the protein catalyses transport of water across membranes.
Figure 3.71 Evidence for presence of aquaporins (water channels) in plant membranes. (a) Change in volume of Xenopus oocytes injected with two TIP proteins after lowering osmotic pressure of the external medium (Maurel et al. 1995). (b) Sensitivity of two TIP proteins expressed in Xenopus oocytes to mercuric chloride (HgCl2), a general inhibitor of aquaporins (Daniels et al. 1996). (c) Inhibitory effect of HgCl2 on hydraulic conductivity of the freshwater alga Chara corallina measured with a pressure probe (Schütz and Tyerman 1997).
Water channels can be inhibited by mercuric chloride when expressed in Xenopus occytes (Figure 3.71b), and also in plant cells (Figure 3.71c). Inhibition is reversed by applying mercaptoethanol to block the action of HgCl2. Under mercury inhibition, the activation energy of water flow increases markedly indicating that water flow is now restricted to diffusional flow across the lipid bilayer, that is, aquaporins are blocked.
Plants have many aquaporin genes. For example, Arabidopsis thaliana has 35 and rice (Oryza sativa) has 33. Proteins encoded by aquaporin genes are localized in the plasma membrane, tonoplast and endo membranes and classed as Plasma membrane Intrinsic Proteins (PIPs), Tonoplast Intrinsic Proteins (TIPs), Nodulin26-like Intrinsic Proteins (NIPS), Small basic Intrinsic Proteins (SIPs) or X Intrinsic Proteins (XIPs) (Luu and Maurel 2013). Within membranes, clustering of PIPs in membrane rafts has been observed, and there is variation in the lateral mobility for different aquaporins. Of the many aquaporin proteins in plants, some transport water only (up to 109 molecules per second) and others are permeable to a range of neutral solutes such as gases (carbon dioxide, ammonia), metalloids (boron, silicon, arsenic), or reactive oxygen species (hydrogen peroxide). The transcription, translation, trafficking, and gating of PIPs are regulated by environmental and developmental factors involving signalling molecules, phytohormones and the circadian clock (Chaumont and Tyerman 2014). The transcription, translation, trafficking, and gating of PIPs are regulated by environmental and developmental factors involving signalling molecules, phytohormones and the circadian clock (Chaumont and Tyerman 2014).
When PIP genes are transcribed, their mRNA is translated in the rough endoplasmic reticulum (ER), and the proteins targeted to the plasma membrane. PIPs belonging to the PIP2 group form homo-oligomers, or hetero-oligomers by associating with PIP1 isoforms. Some PIP2s contain a diacidic motif in their N terminus that acts as an ER export signal. It may be recognized by Sec24 which is the main “cargo” selection protein of the coat protein complex COPII that mediates vesicle formation at the ER export sites. PIP oligomers then transit through the Golgi apparatus and trans-Golgi network and are then loaded into secretory vesicles and routed to the plasma membrane (Figure 3.72). Insertion of PIPs into the plasma membrane is mediated by a protein that regulates vesicle fusion (the “syntaxin” SYP121). The plasma-membrane localized PIPs can be recycled internally: once internalized in vesicles, PIPs are delivered to the trans-Golgi network before being routed back to the plasma membrane or directed into lytic vacuoles for degradation (Figure 3.72). Salt stress causes dephosphorylation and internalization of PIPs, and drought stress induces ubiquitylation of PIPs, which are then degraded in the proteasome.
Aquaporins assemble as homo- or hetero-tetramers, each monomer acting as an independent water channel. The structure of an aquaporin monomer (Figure 3.72) consists of six membrane-spanning α-helices connected by five loops, with both N and C termini facing the cytosol. Two loops form two short hydrophobic α-helices dipping halfway into the membranes, which, together with the membrane-spanning helices, create a pore with high specificity (Murata et al. 2000).
Figure 3.72 Formation and trafficking of PIPs within a plant cell. PIPs belonging to the PIP2 group (in yellow) form homo- or heterooligomers by associating with PIP1 isoforms (in green). PIP oligomers transit through the Golgi apparatus and trans-Golgi network (TGN) and are then loaded into secretory vesicles and routed to the plasma membrane. In the circle is shown the topological structure of the aquaporin monomer AQP1 (Murata et al. 2000), with six membrane-spanning α-helices (1-6) connected by five loops (A-E). The loops B and E form two short hydrophobic α-helices (in red) dipping halfway into the membranes, which, together with the membrane-spanning helices, create a pore with high specificity. From Chaumont and Tyerman (2014). Reproduced from F. Chaumant and S.D. Tyerman, Plant Phys 164: 1600-1618, plantphysiol.org. Copyright American Society of Plant Biologists.
Aquaporins play a central role in regulating plant water relations. Water diffusion across cell membranes is facilitated by aquaporins that provide plants with the means to rapidly and reversibly modify water permeability. This is done by changing aquaporin density and activity in the membrane, including post-translational modifications and protein interaction that act on their trafficking and gating. At the whole organ level aquaporins modify water conductance and gradients at key “gatekeeper” cell layers that impact on whole plant water flow and plant water potential. In this way they may act in concert with stomatal regulation.
PIP and TIP expression is higher during the day than the night, and correlates with diurnal changes in transpiration. It is likely under circadian regulation. Expression can correlate with changes in hydraulic conductivity, Lp, so that aquaporins are more abundant or have higher activity at times when stomatal conductance is higher. Over a diurnal cycle, Lp can change 2-5 fold and so can PIP transcript activity or protein abundance (Chaumant and Tyerman 2014). This occurs in both roots and shoots.
This section has shown how the flow of water and ions across membranes are linked. The function of membrane transport in regulating nutrient supply is covered in Chapter 4.
