Ions such as potassium and chloride (K+ and Cl–) are major osmotic solutes in plant cells. Deficiency of either of these two nutrients can increase a plant’s susceptibility to wilting. Most other inorganic nutrients are acquired as ions and some major organic metabolites involved in photosynthesis and nitrogen fixation bear a charge at physiological pH. For example, malic acid is a four-carbon organic acid that dissociates to the divalent malate anion at neutral pH. Calcium (Ca2+) fluxes across cell membranes are involved in cell signalling and although not osmotically significant they play a crucial role in the way cells communicate and self-regulate. Finally, some ions are used to store energy but need not occur at osmotically significant concentrations. Cell membranes from all kingdoms use hydrogen (H+) ions (protons) in one way or another to store energy that can be used to move other ions or to manufacture ATP (Chapter 2). The highest concentration of H+ that occurs is only a few millimoles per litre yet H+ plays a central role in energy metabolism.
To understand ion movement across membranes, two crucial points must be understood: (1) ionic fluxes alter and at the same time are determined by voltage across the membrane; (2) in all solutions bounded by cell membranes, the number of negative charges is balanced by the number of positive charges. Membrane potential is attributable to a minute amount of charge imbalance that occurs on membrane surfaces. So at constant membrane potential the flux of positive ions across a membrane must balance the flux of negative ions. Most biological membranes have a capacitance of about 1 microFarad cm–2 which means that to alter membrane voltage by 0.1 V, the membrane need only acquire or lose about 1 pmol of univalent ion cm–2 of membrane. A univalent ion is one with a single positive (e.g. K+) or negative (e.g. Cl–) atomic charge. In a plant cell of about 650 pL, this represents a change in charge averaged over the entire cell volume of 12 nmol L–1!
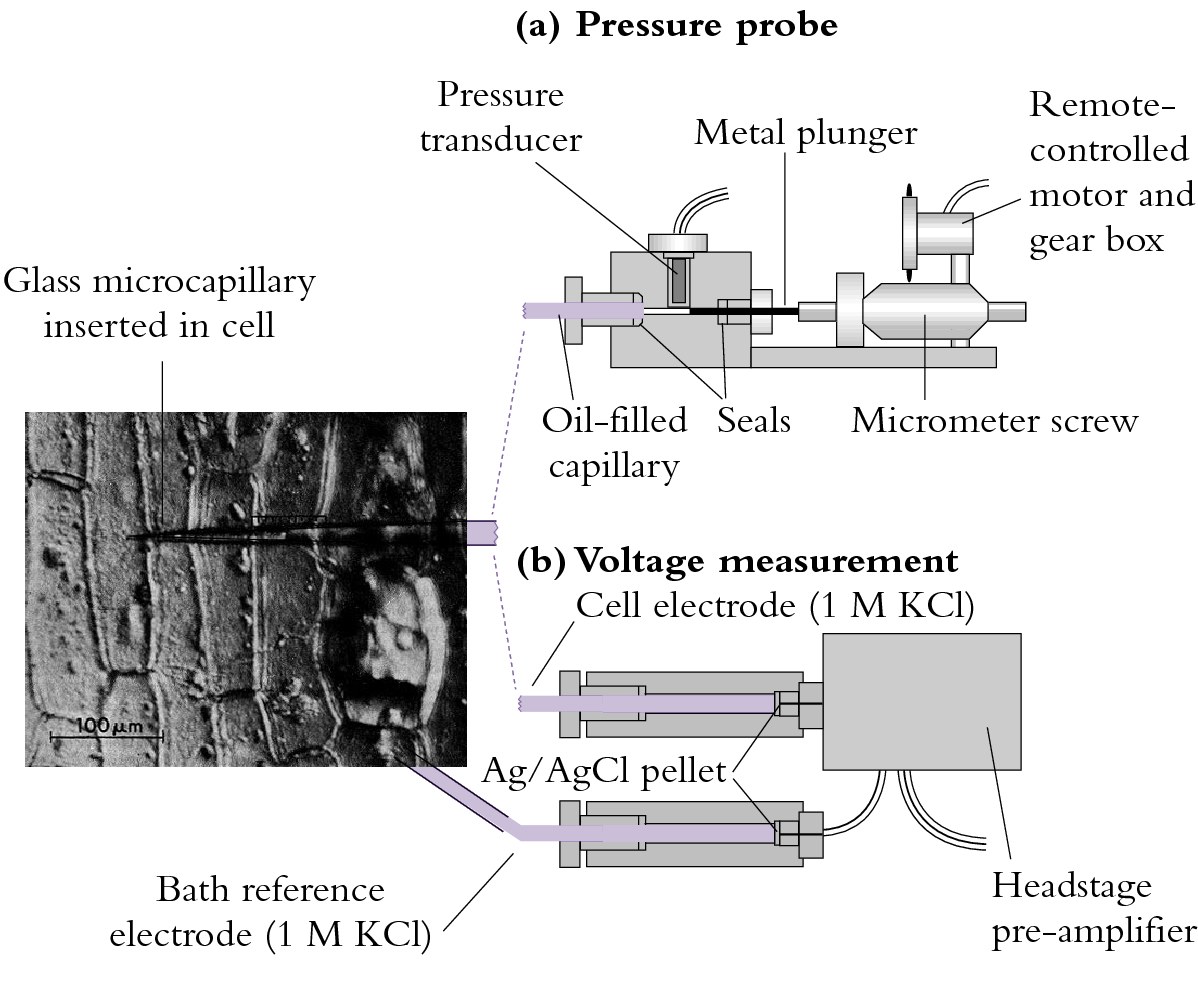
The membrane voltage or membrane potential difference, as it is sometimes called, can be measured by inserting a fine capillary electrode into a plant cell (Figure 3.68b). Membrane voltage is measured with respect to solution bathing the cell and in most plant cells the voltage is negative across the plasma membrane. That is, the cytoplasm has a charge of –0.1 to –0.3 V (–100 to –300 mV) at steady state with occasional transients that may give the membrane a positive voltage. The tonoplast membrane that surrounds the central vacuole is generally 20 to 40 mV more positive than the cytoplasm (still negative with respect to the outside medium).
Figure 3.68. (a) Techniques employing fine glass capillaries to probe plant cells. (b) A probe for measuring membrane voltage. The capillary is filled with 1 mol L-1 KCl and connected to a silver/silver chloride electrode that acts as an interface between solution voltage and input to the amplifier. A voltage is always measured with respect to a reference (in this case, a bath electrode). The headstage amplifier is close to the electrodes to minimise noise.
Cell membrane voltages can be affected by ion pumps, diffusion potential and fixed charges on either side of the membrane.
Special mention needs to be made of one such fixed charge which arises from galacturonic acid residues in cell walls. Although cations move to neutralise this fixed negative change, there is still a net negative potential associated with cell walls (Donnan potential). In spite of being external to the plasma membrane, the Donnan potential is in series with it and probably adds to what we measure as the membrane potential with electrodes.
Most charge on macromolecules in the cytoplasm is also negative (e.g. nucleic acids, proteins) and because of their size it can be regarded as a fixed negative charge. This has consequences on the water relations of the cytoplasm in that they exert a significant osmotic potential, even though not in solution, as do the clay particles in soil (Passioura 1980).
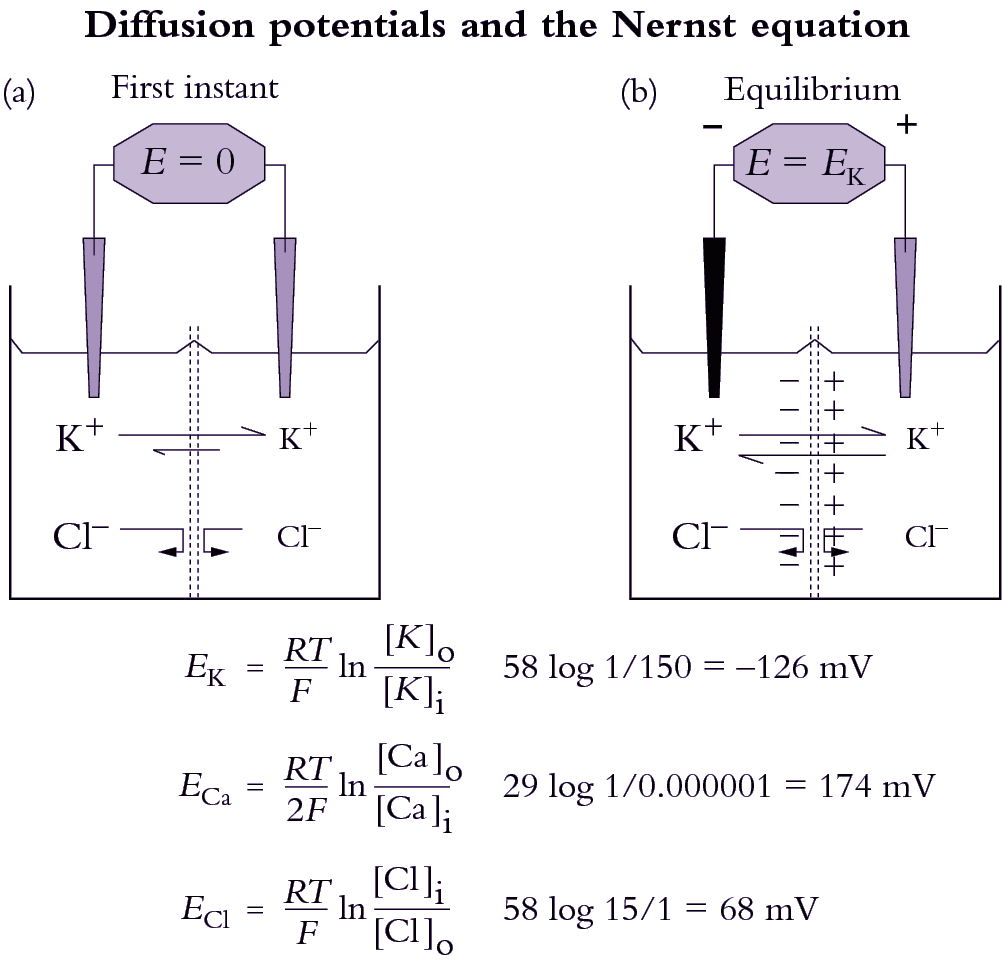
Different ions have different permeabilities in membranes. Potassium, for example, is usually the most permeable ion, entering under most conditions about 10 to 100 times faster than Cl– Since ions diffuse at different rates across membranes, a slight charge imbalance occurs and gives rise to a membrane voltage (Figure 3.69). This voltage in turn slows down movement of the rapidly moving ion so that the counter-ion catches up. The result is that when net charge balance is achieved, a diffusion potential has developed that is a function of the permeabilities (\( P_\text{ion} \)) of all diffusible ions present and concentrations of each ion in each compartment.
Figure 3.70. How a diffusion potential develops through differential movement of an ion across a membrane that is permeable to K+ but not Cl-. The left hand compartment (representing the cytoplasm) has the higher concentration of K+ and Cl-, as indicated by the size of the letters. The right hand compartment represents the apoplast (cell wall). Initially (a), a minute amount of K+ crosses the membrane along its concentration gradient, and creates a positive charge in the right-hand compartment as K+ concentration there rises above Cl- concentration. At equilibrium (b), a diffusion potential is established, and further movement of K+ is prevented. Concentrations never equalise on both sides because K+ is the only species able to move through the membrane.
The Goldman equation describes this phenomenon and gives the membrane voltage (\( \Delta E \) ) that would develop due to diffusion of ions. The Goldman equation for the ions that mostly determine this diffusion potential (K+, Na+ and Cl–) is given by:
\[ \Delta E = \frac{RT}{F} \ln \frac{P^{}_K C_K^o + P^{}_{Na}C_{Na}^o + P^{}_{Cl}C_{Cl}^i}{P^{}_K C_K^i + P^{}_{Na}C_{Na}^i + P^{}_{Cl}C_{Cl}^o} \tag{17}\]
The superscripts refer to the inside (i) or outside (o) of the membrane and \( R \), \( T \), \( F \) and \( C \) are defined elsewhere (Equation 4.5). Note that the concentration terms for Cl– are reversed in the numerator and denominator compared to the cations. This is because Cl– is the only anion represented. Many texts do not include H+ in the Goldman equation because, in spite of high permeability of H+, diffusion of H+ is unlikely to have a strong effect on ΔE at such low (micromolar) concentrations. However, membrane potential is occasionally dominated by the diffusion of H+, indicating that H+ permeability must be exceedingly high. For example, local variations in pH cause alkaline bands to form on Chara corallina cells and in the leaves of aquatic plants at high pH.
When one ion has a very high permeability compared to all other ions in the system the membrane will behave as an ion-sensitive electrode for that ion (e.g. Figure 4.7). A pH electrode which is sensitive to H+ flux across a glass membrane serves as an analogy. In the case of a single ion, the Goldman equation can be reduced to the simpler Nernst equation that yields the equilibrium membrane potential which would develop for a particular concentration gradient across a membrane.
\[ \Delta E = \frac{RT}{zF} \ln \frac{C_o}{C_i} \tag{18}\]
where \( R \) and \( T \) are the gas constant and temperature (degrees Kelvin) and \( F \) is the Faraday constant. Typical charges on ions (\( z \)) would be –1 for Cl-, +1 for K+) and so on. This term in the Nernst equation gives the correct sign for the calculated membrane potential.
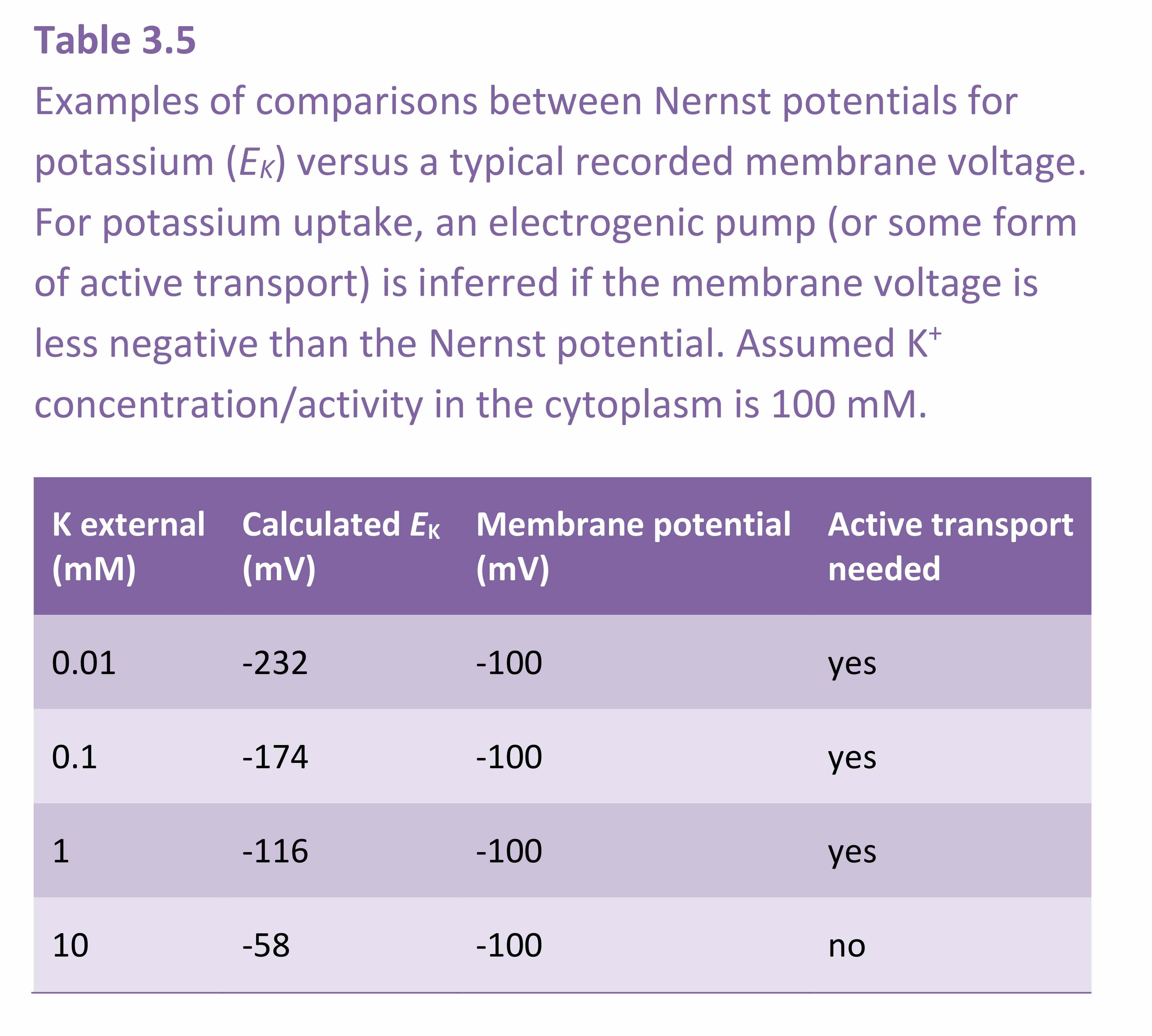
The Nernst equation is routinely used by electro-physiologists to calculate the equilibrium potential for each ion. Theoretical equilibrium potentials can then be compared with the actual membrane potential in order to decide whether the membrane is highly permeable to one particular ion. For example, in many plant cells there are K+ channels that open under particular circumstances. When this occurs, the membrane becomes highly permeable to K+ and the measured membrane potential very nearly equals the Nernst potential for K+. The Nernst equation can also be used as a guide in deciding whether there is active transport through a membrane. For example, when the measured membrane potential is less negative than the most negative Nernst potential, an electrogenic pump must be engaged for K+ to enter the cell (Table 4.1). If the membrane potential is less negative than the Nernst potential and if a K+ channel were open then K+ would leak out of the cell. For K+ uptake to occur with such a gradient for passive efflux then energy would need to be generated.
Equation 4.7 can be rewritten with constants solved and log10 substituted for the natural logarithm. This yields a useful form as follows,
\[ \Delta E = \frac{58}{z} \log_{10} \frac{C_o}{C_i} \tag{19} \]
showing that 10-fold differences in concentration across a membrane are maintained by a 58 mV charge separation for monovalent ions. For example, -58 mV will keep K+ concentrations 10 times higher inside a cell than in the external medium and Cl– concentrations 10 times lower. Plasma membranes are normally about -116 mV, which would keep K+ concentrations inside a cell 100 times higher and Cl- concentrations 100 times lower than in the external solution.
Internal membranes have a different electrical potential, the mitochondria being more negative than the plasma membrane (around -180 mV) and the chloroplast and tonoplast being slightly positive (around +50 mV).
The concentration of an ion inside a cell membrane (\( C_i \)) that would occur at equilibrium for any \( C_o \) and \( \Delta E \) can be calculated by rearranging the above equation as:
\[ \log_{10} C_i = \log_{10} C_o - \frac{z\Delta E}{58} \tag{20} \]
remembering that \( z \) and \( \Delta E \) can be positive or negative, depending on the ion and the particular cell membrane being considered.
