Figure 3.1 Surface view of cleared whole mount of a wheat leaf showing large and small parallel veins (mauve) with transverse veins connecting them. Lines of stomates (shown by the orange colour of the guard cells) lie along the flanks of these veins. Water evaporates from the wet walls of mesophyll cells below the stomates, drawing water from the veins. Distance between veins is 0.15 mm; scale bar is 100 µm. (Photograph courtesy M. McCully)
Water is often the most limiting resource determining the growth and survival of plants. This can be seen in both the yield of crop species and the productivity of natural ecosystems with respect to water availability.
The natural distribution of plants over the earth’s land surface is determined chiefly by water: by rainfall (\( R \)) and by evaporative demand (potential evapotranspiration, \( PE \)) which depends on temperature and humidity. This leads to such diverse vegetation groups as the lush vegetation of tropical rainforests, the shrubby vegetation of Mediterranean climates, or stands of tall trees in temperate forests. Climates can be classified according to the Thornthwaite Index: \( (R-PE)/PE \).
Agriculture also depends on rainfall. Crop yield is water-limited in most regions in the world, and agriculture must be supplemented with irrigation if the rainfall is too low. Horticultural crops are usually irrigated.
Plants require large amounts of water just to satisfy the requirements of transpiration: a large tree may transpire hundreds of litres of water in a day. Water evaporates from leaves through stomates, which are pores whose aperture is controlled by two guard cells. Plants must keep their stomates open in order to take up CO2 as the substrate for photosynthesis (Chapter 2). In the process, water is lost from the moist internal surfaces of the leaf through the stomatal pores (Figure 3.1). Water loss also has a benefit in maintaining the leaf temperature through evaporative cooling.
The ratio of water lost to CO2 taken up is around 300:1 in most land plants, meaning that plants must transpire large quantities of water on a daily basis in order to take up sufficient CO2 for normal development.
In this section we will examine plant water relations and the variables that plant physiologists use to describe the status and movement of water in plants, soil and the atmosphere.
One of the challenging aspects of understanding plant water relations is the range of pressures from positive to negative that occur within different tissues and cells. Positive pressures (turgor) occur in all living cells and depend on the semipermeable nature of the plasma membrane and the elastic nature of the cell walls. Negative pressures (tensions) occur in dead cells and depend on the cohesive strength of water coupled with the strength of heavily lignified cell walls to resist deformation. These play an important role in water transport through the xylem.
Figure 3.3 Wilted squash plants demonstrating loss of cell turgor. (Photograph courtesy of Home and Garden Information Center, University of Maryland Extension).
Well-watered plants are turgid, and their leaves and stems are upright and firm, even without woody tissue to support them. If water is lost from leaves through the stomates at a faster rate than it is resupplied by roots, then plants wilt (Figure 3.3)
Well-watered plants are turgid because their cells are distended by large internal hydrostatic pressures (Figure 3.4a). This internal hydrostatic pressure (also called turgor pressure) is typically 0.5 MPa or more. Lack of water causes cells to shrink until the pressure inside equals that of the atmosphere (zero), and the cells thus have zero turgor (Figure 3.4b). The initial shrinkage while turgor drops from 0.5 to zero MPa is determined by the properties of the cell wall: cell walls are slightly elastic, and the relation between volume change and turgor pressure depends on the “elastic modulus” of the wall. This involves little change in whole cell volume for a drop in turgor pressure to zero. However, further water loss causes the wall to shrink and deform inwards, and the whole cell volume decreases markedly.
Figure 3.4 Turgid leaf cell and flaccid cell (zero turgor). (a) In the turgid cell in a well-watered plant, the cell is distended by a large internal hydrostatic pressure, usually 0.5 MPa - 1 MPa. (b) In the flaccid cell of a wilted plant, the cell wall is rather dry, and water has been lost to the atmosphere until the pressure inside is that of the atmosphere, zero.
The turgor pressure of a fully turgid cell may even exceed 1 MPa, about five times the pressure in a car tyre, and ten times the pressure in the atmosphere. In a physically unconstrained cell, the turgor pressure is borne by the cell wall, which develops a large tension within it. But in cells that are physically constrained, such as those of a tree root whose growth becomes hampered by the presence of a slab of concrete, the tension in the cell walls is relieved and the pressure is applied directly to the constraint (Figure 3.5).
Figure 3.5 Roots lifting slab of concrete. (Photograph courtesy L. Atmore, Daily Bruin, UC Davis)
It is easy to see how a constrained tree root could eventually lift a slab of concrete: 1 MPa applied over 100 cm2 is equivalent to a weight of one tonne. Pressure is force/area, and 1 MPa is approximately equal to 10 kg weight per cm2.
A definition of all these terms is summarised at the end of this section (Section 3.1.7).
How is it that plant cells can have such large turgor pressures? The essential reason is that the cells contain large concentrations of solutes. These solutes attract water into the cells through a process known as osmosis, which involves water flowing in through semipermeable membranes that prevent the passage of solutes but not of water. The inflow of water swells the cells until a hydrostatic pressure is reached at which no more water will flow in. In cells bathed in fresh water, such as algal cells in a pond, this equilibrium hydrostatic pressure is known as the osmotic pressure (\( \pi \)) of the cell contents, and is commonly about 500 kPa or 0.5 MPa.
This osmotic pressure can be measured directly with an osmometer, or it can be calculated from the solute concentration in the cell (\( C \)) from the van‘t Hoff relation:
\[ \pi = RTC \tag{1} \]
where \( R \) is the gas constant, \( T \) is the absolute temperature (in degrees Kelvin) and \( C \) is the solute concentration in Osmoles L-1. At 25 ºC, \( RT \) equals 2.5 litre-MPa per mole, and \( \pi \) is in units of MPa. Hence a concentration of 200 mOsmoles L-1 has an osmotic pressure of 0.5 MPa.
However, land plants are different from algae in a pond. Their leaves are in air, and the water in their cell walls, unlike the water in a pond, is not free. It has a negative hydrostatic pressure (discussed further in the next section). Thus, for a given osmotic pressure (\( \pi \)) within a cell, the hydrostatic pressure, \( P \), will be lower than if the cell were bathed in free water. This difference is known as the water potential (\( \psi \)) of the cell. It is zero in an algal cell in fresh water, but it is always negative in land plants. Its value is the difference between \( P \) and \( \pi \), that is:
\[ \psi=P-\pi \tag{2} \]
An alternative notation for equation (2) used commonly by plant physiologists is:
\[ \psi_w = \psi_p + \psi_s \tag{3} \]
In this case, \( \psi_w \) is the total water potential, \( \psi_s \) is the solute potential and \( \psi_p \) is the pressure potential. Thus \( \psi_s \) is equal, but opposite in sign, to \( \pi \).
The notion of water potential can be applied to any sample of water, whether inside a cell, in the cell wall, in xylem vessels, or in the soil. Water will flow from a sample with a high water potential to one with a low water potential provided the samples are at the same temperature and provided that no solutes move with the water. Water potential thus defined is always zero or negative, for by convention it is zero in pure water at atmospheric pressure.
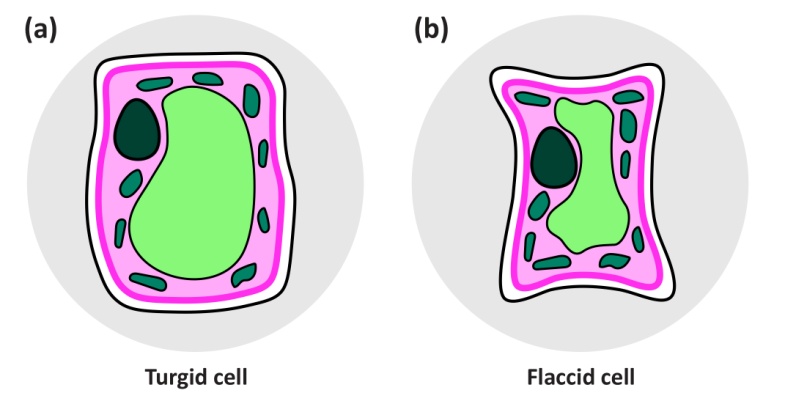
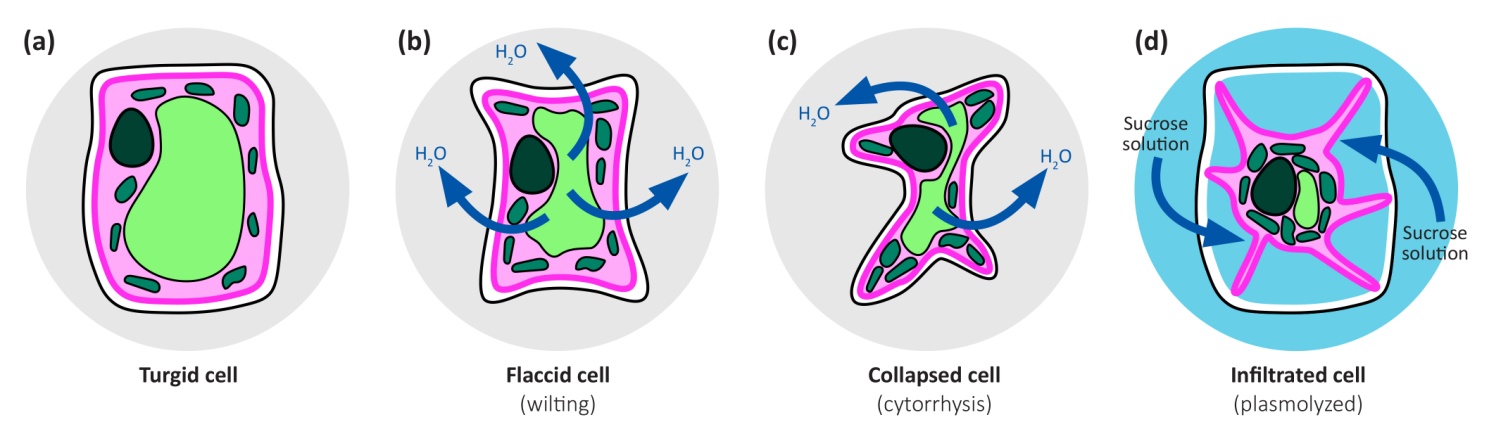
Positive values of hydrostatic pressure occur in the living cells of plants, in the symplast, and as explained above are induced by high solute concentrations and the resultant osmotic pressure. However, large negative values are common in the apoplast of plants and the soil they are growing in. These negative values arise because of capillary effects - the attraction between water and hydrophilic surfaces at an air/water interface, the effects of which can be seen in the way that water wicks into a dry dishcloth. This attraction reduces the pressure in the water, and does so more intensely the narrower are the water-filled pores. It accounts for how cell walls, which have very narrow pores, can remain hydrated despite very low water potentials in the tissue they are part of. For a geometrically simple cylindrical pore, the relation between the induced pressure and the radius of the pore can be derived as follows:
Take a glass capillary tube with a radius \( r \) (m) and place it vertically with one end immersed in water. Water will rise in the tube against the gravitational force until an equilibrium is reached at which the weight of the water in the tube is balanced by the force of attraction between the water and the glass. A full, hemispherical, meniscus will have now developed, i.e. one with a radius of curvature equal to that of the tube (Figure 3.6).
Figure 3.6 A fully-developed meniscus in a cylindrical tube showing the equality between the upward pull of surface tension and the downward pull of the suction in the water from which the relation \( \Delta P = 2\gamma/r \) can be derived.
The meniscus is curved because it is supporting the weight of the water - much as a trampoline sags when several people are sitting on it. There is a difference in pressure, \( \Delta P \) (Pa), across the meniscus, with the pressure in the water being less than that of the air. The downward acting force (N) on the meniscus is the difference in pressure multiplied by the cross-sectional area of the tube, i.e \(\pi r^2 \Delta P\). The upward acting force is equal to the perimeter of contact between water and glass (\( 2 \pi r \)) multiplied by the surface tension, \( \gamma \) (N m-1), of water, namely \( 2 \pi r \gamma \) (provided the glass is perfectly hydrophilic, when the contact angle between the glass and the water is zero, otherwise this expression has to be multiplied by the cosine of the angle of contact). Thus, because these forces are equal at equilibrium, we have \(\pi r^2 \Delta P = 2 \pi r \gamma \), whence
\[ \Delta P = 2\gamma/r \tag{4}\]
The surface tension of water is 0.075 N m-1 at about 20°C, so \( \Delta P \) (Pa) equals 0.15 divided by the radius \( r \) (m):
\[ \Delta P = 0.15/r \tag{5}\]
Thus a fully-developed meniscus in a cylindrical pore of radius 0.15 mm would have a pressure drop across it of 1.0 MPa. The pressure, \( P \), in the water would therefore be -1.0 MPa if referenced to normal atmospheric pressure, or -0.9 MPa absolute pressure (given that standard atmospheric is approximately 100 kPa).
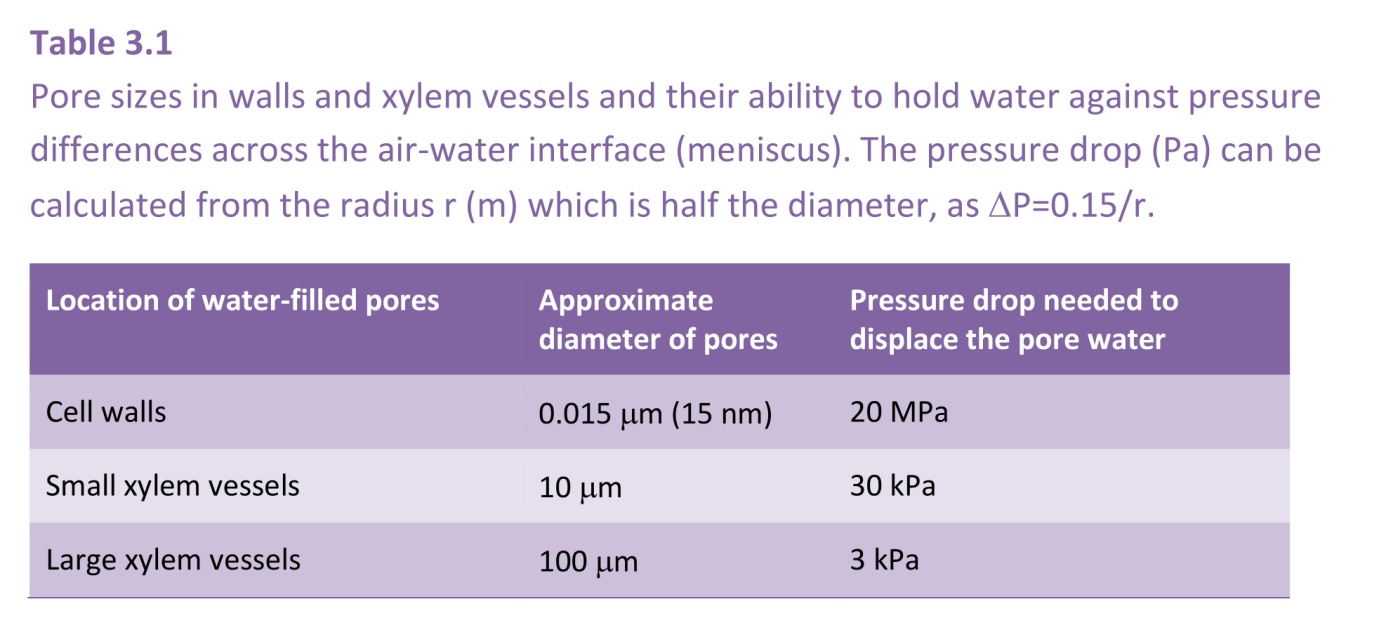
This argument applies not only to cylindrical pores. It is the curvature of the meniscus that determines the pressure drop, and this curvature is uniform over a meniscus occupying a pore of any arbitrary shape. It is such capillary action that generates the low pressures (large suctions) in the cell walls of leaves that induce the long-distance transport of water from the soil through a plant to the sites of evaporation. The pores in cell walls are especially small (diameters of the order of 15 nm), and are therefore able to develop very large suctions, as they do in severely water-stressed plants. Such pores can hold water against a suction of 10 MPa. (Table 3.1)
In plants, other water-filled pores vary in size from large xylem vessels with diameters of 100 mm or more down to a few mm, so for them to remain water-filled requires that they have no air/water interfaces.
When a cell in an intact plant growing in soil loses water, turgor declines and solute concentrations increase. As explained before (3.1.1), at turgor loss point, when turgor becomes zero, the hydrostatic pressure in the cell sap is equal to the atmospheric pressure, meaning that no net force is exerted on the cell wall, and the plant is wilting. If water continues to be lost from the cell, the pressure within the cytoplasm drops below atmospheric pressure, resulting in a force imbalance that collapses the cell wall. The deformation of living cells upon desiccation is called cytorrhysis. Note that the plasma membrane remains in close contact with the cell wall throughout desiccation ie plasmolysis does not occur, because the hydrostatic pressure in the cytoplasm remains greater than the hydrostatic pressure in the apoplast.
Plasmolysis only occurs in cells that are completely immersed in solution and have no air spaces around them, as in epidermal strips floating on water. Plasmolysis starts when the osmotic pressure of the solution is increased above that of the cells, causing the protoplast to shrink, and the plasma membrane separates from the wall (Fig. 3.7). Large gaps created between the plasma membrane and the wall fill with the bathing solution. This cannot occur in normal tissues as the cells have air spaces between them that are not filled with water. This includes root cells of intact plants growing in hydroponic solution or in waterlogged soil, as they still have air spaces.
Air cannot enter the cell through the cell walls as the small pore size, about 15 nm, would need a suction of 20 MPa to drain the pores (Table 3.1, in previous section) which is impossible.
Figure 3.7. Turgid leaf cell (turgor about 0.5 MPa) and flaccid cell (zero turgor) that has lost some water. With further water loss, the cell collapses. The collapse of the wall is called cytorrhysis. Plasmolysis occurs when a cell is placed in a solution of osmotic strength greater than that of the cell. Water is withdrawn from the cell until its concentration of solutes equals that of the bathing solution. If the bathing solution is sucrose or NaCl or any small molecule (smaller than the pores in the cell wall), solution enters the cell through pores in the cell wall which prevents cytorrhysis.
During plasmolysis, the plasma membrane is stretched into strands that remain tethered to the wall at particular sites (Figure 3.8). Plasmolysis has been used by microscopists to demonstrate the tethering of the plasma membrane to specific sites on cell walls, by floating tissue such as epidermal peels of onion bulbs on high concentration of solution of sucrose (Figure 3.8). When the protoplast shrinks away from the cell wall, and solution with small molecular weight solutes pentrates the cell wall and floods into the space between the wall and the proplasts, some parts of the plasma membrane stay tethered and the rest become pulled into very fine strands.
Figure 3.8. Cells in onion bulb scale leaf epidermis before and after plasmolysis, viewed by confocal microscopy and stained with fluorescent dye DIOC(6). (A) Cytoplasm is seen as pale strands at the cell surface, traversing the large vacuole. Cell boundaries are bright because the surface cytoplasm is intensely fluorescent. (B) Precisely the same field of view after plasmolysis in 0.6 M sucrose. The cell walls are now visible as dark lines between the shrunken protoplasts, which still show brightly fluorescent surfaces. (C) A reconstruction of many planes of focus at higher magnification to show some of the hundreds of stretched strands of plasma membrane that remain tethered to the wall during plasmolysis. (Micrographs courtesy B.E.S. Gunning)
The difference between cytorrhysis versus plasmolysis is most easily seen in leaves with single cell layers like mosses. Figure 3.9 shows that in the hydrated leaflet of Physcomytrella, when the central vacuole is distended, the chloroplasts line the cell wall. Rapid water loss causes a general shrinkage and eventually a collapse at the central parts of the cells. In cytorrhysis, the plasma membrane always remains in close contact with the cell wall. In contrast, when cells are bathed in a solution of small molecules like sucrose, glycerol, or low molecular weight polyethylene glycol, PEG, the solutes pass through the cell wall but not the plasma membrane, causing shrinkage of the protoplast and detachment of the plasma membrane from the cell wall. In plasmolysis, the gaps between the cell wall and the plasma membrane are filled with plasmolytic solution (Figure 3.9).
Figure 3.9. Cytorrhysis versus plasmolysis in Physcomitrella patens. Left: The single cell layer of a hydrated moss leaflet. Centre: Cytorrhysis, where water loss causes a general shrinkage and eventually a collapse at the central parts of the cells. White areas appear where the upper and lower cell walls meet; the chloroplasts are pushed towards the side walls. Right: Plasmolysis in 10% glycerol, which passes through the cell wall but not the plasma membrane. Water loss causes shrinkage of the living protoplast and the detachment of the plasma membrane from the cell wall. (Photographs courtesy I. Lang)
Cytorrhysis also occurs during freezing, when water is withdrawn from cells (Buchner and Neuner 2010).
Plasmolysis is a laboratory phenomenon and does not occur in nature. It is an experimental artifact.
Water flows throughout the plant in three different ways: (a) in bulk, (b) by diffusion in a liquid, and (c) by diffusion as a vapour. Different mechanisms are involved in these three types of flow.
Bulk flow is driven by gradients in hydrostatic pressure. It is much faster than diffusive flow because the molecules are all travelling in the same direction and hence their movement is cooperative. This is the flow that occurs in xylem vessels, in the interstices of cell walls, and in water-filled pores in soil. The resistance to such flow depends very strongly on the size of the flow channels.
Tall trees and fast-growing cereal crops like maize have large xylem vessels, of 100 µm in diameter or more. Flow rates are fast because the rate of volume flow increases in proportion to the fourth power of the radius for a given pressure gradient. Volume flow rate (m3s-1) in a cylindrical tube of radius \( r \) is proportional to \( r^4 \) and to the gradient in pressure along the tube, and inversely proportional to the viscosity \( η \) (Pa s) (Poiseuille’s Law)
\[ \text{Volume flow rate} = \left(\frac{\pi r^4}{8\eta}\right) * \left(\frac{\Delta P}{\Delta x}\right) \tag{6}\]
Where \( η \) is the solution viscosity and \( ΔP/Δx \) (Pa m-1)is the gradient in hydrostatic pressure. From equation (5) we understand that wide tubes are enormously more effective than narrow tubes. The importance of the relationship between tube radius and conductive efficiency becomes apparent when we examine long distance transport of water through the xylem (Section 3.2).
Diffusive flow in the liquid phase is driven by gradients in osmotic pressure. It is much slower than bulk flow because the net flows of solute and water molecules are in opposite directions and therefore impede each other. Where two liquid phases are separated by a semi-permeable membrane the flow of water across the membrane to the phase with the higher osmotic pressure is essentially diffusive, and the flow is driven by the difference in water potential across the membrane.
Vapour flow, for example through the stomata, is driven by gradients in vapour concentration, which are usually expressed in terms of partial pressure, but are nevertheless mechanistically concentrations.
As water in the transpiration stream moves from the soil to the roots, through the plant, and out through the stomata, all three types of flow are involved at various stages.
The potential energy of water is affected by gravity: unconstrained water runs down hill. In most plants the effect of gravity is small relative to common values of the water potential, but in tall trees it can dominate. Where the effect is important it is convenient to introduce the notion of a total water potential, \( Φ \), which is the sum of the water potential, \( ψ \), and a gravitational term, thus
\[\Phi = \psi + \rho gh = P - \pi + \rho gh \tag{7}\]
where \( ρ \) (kg m-3) is the density of water, \( g \) (m s-2) is the acceleration due to gravity, and \( h \) (m) is the height (relative to some reference) in the gravitational field. \( Φ \) is constant in a system at equilibrium with respect to water even when height varies. The value of \( g \) is approximately 10 m s-2, so the gravitational term, \( ρgh \), increases by 10 kPa for each metre increase in height. Hence, at equilibrium, when \( Φ \) and \( π \) are uniform (at least, in a system without semipermeable membranes) the hydrostatic pressure falls by 10 kPa for each metre increase in height.
In the tallest trees, for example a Eucalyptus regnans 100 m tall, equation (6) predicts that, even when the tree is not transpiring, the water potential at the top is about 1.0 MPa lower than at the base.
Pressure is force per unit area, Newtons per square meter, or N m-2. Its unit is the Pascal (Pa). 1 MPa is approximately equal to 10 kg weight per cm2.
Hydrostatic pressure is the pressure in a stationary fluid. (Note that hydrostatic pressure is usually quoted as the difference from atmospheric pressure, and is therefore taken to be zero when it equals atmospheric pressure).
Turgor pressure is the term used for the hydrostatic pressure in the cells’ contents.
Osmotic pressure (\( π \)) is the hydrostatic pressure in a compartment containing an aqueous solution that will just prevent pure water at atmospheric pressure flowing into that compartment through its membrane that is permeable to the water but not to the solutes within.
Water potential is the difference between \( P \) and \( π \).
Kramer PF, Boyer JS (1995) Water relations of plants and soils. http://udspace.udel.edu/handle/19716/2830
Nobel PS (2005) Physicochemical and environmental plant physiology (3rd edition). Elsevier Academic Press, Burlington, MA
Passioura JB (1980) The meaning of matric potential. J Exp Bot 31:1161-1169
Passioura JB (2010) Plant–Water Relations. In: Encyclopedia of Life Sciences. Wiley, Chichester. DOI: 10.1002/9780470015902.a0001288.pub2
