3.0-Ch-Fig-3.3.jpeg
Figure 3.3 Wilted squash plants demonstrating loss of cell turgor. (Photograph courtesy of Home and Garden Information Center, University of Maryland Extension).
Well-watered plants are turgid, and their leaves and stems are upright and firm, even without woody tissue to support them. If water is lost from leaves through the stomates at a faster rate than it is resupplied by roots, then plants wilt (Figure 3.3)
Well-watered plants are turgid because their cells are distended by large internal hydrostatic pressures (Figure 3.4a). This internal hydrostatic pressure (also called turgor pressure) is typically 0.5 MPa or more. Lack of water causes cells to shrink until the pressure inside equals that of the atmosphere (zero), and the cells thus have zero turgor (Figure 3.4b). The initial shrinkage while turgor drops from 0.5 to zero MPa is determined by the properties of the cell wall: cell walls are slightly elastic, and the relation between volume change and turgor pressure depends on the “elastic modulus” of the wall. This involves little change in whole cell volume for a drop in turgor pressure to zero. However, further water loss causes the wall to shrink and deform inwards, and the whole cell volume decreases markedly.
3.0-Ch-Fig-3.4.jpeg
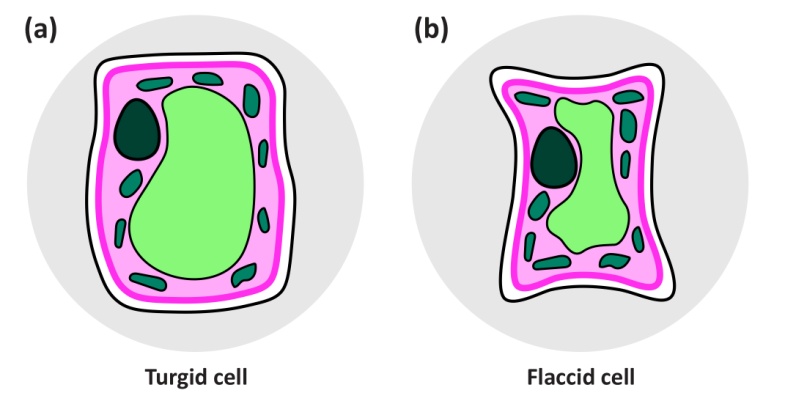
Figure 3.4 Turgid leaf cell and flaccid cell (zero turgor). (a) In the turgid cell in a well-watered plant, the cell is distended by a large internal hydrostatic pressure, usually 0.5 MPa - 1 MPa. (b) In the flaccid cell of a wilted plant, the cell wall is rather dry, and water has been lost to the atmosphere until the pressure inside is that of the atmosphere, zero.
The turgor pressure of a fully turgid cell may even exceed 1 MPa, about five times the pressure in a car tyre, and ten times the pressure in the atmosphere. In a physically unconstrained cell, the turgor pressure is borne by the cell wall, which develops a large tension within it. But in cells that are physically constrained, such as those of a tree root whose growth becomes hampered by the presence of a slab of concrete, the tension in the cell walls is relieved and the pressure is applied directly to the constraint (Figure 3.5).
3.0-Ch-Fig-3.5.png
Figure 3.5 Roots lifting slab of concrete. (Photograph courtesy L. Atmore, Daily Bruin, UC Davis)
It is easy to see how a constrained tree root could eventually lift a slab of concrete: 1 MPa applied over 100 cm2 is equivalent to a weight of one tonne. Pressure is force/area, and 1 MPa is approximately equal to 10 kg weight per cm2.
A definition of all these terms is summarised at the end of this section (Section 3.1.7).