Phloem flux can be estimated in a number of ways. The simplest is to determine dry weight gain of a discrete organ connected to the remainder of a plant by a clearly definable axis of known phloem cross-sectional area. Developing fruits or tubers meet these criteria. Sequential harvests from a population of growing fruit or tubers provide measures of the organ’s net gain of dry matter imported through the phloem. Net gains or losses of dry matter resulting from respiration or photosynthesis are incorporated into calculations to give gross gain in dry matter by the organ. Flux of dry matter through the phloem (specific mass transfer — SMT; Canny 1973) can then be computed on a phloem or preferably on a sieve-tube lumen cross-sectional area basis. Area estimates can be obtained from histological sections of the pedicel or stolon that connects a test organ to its parent plant. Expressed on a phloem cross-sectional area basis, SMT estimates are normally in the range of 2.8–11.1 g m–2 phloem s–1 (Canny 1973). Flux on the basis of sieve-tube lumen cross-sectional area is preferable but relies on identification of sieve tubes and the assumption that they are equally functional as transport conduits. Sieve tubes account for some 20% of phloem cross-sectional area, suggesting fluxes are about five-fold higher through a sieve-tube lumen.
Speed of phloem translocation can be determined from simultaneous measurements of SMT and phloem sap concentrations as shown in Equation 5.1 below:
\[\mathrm{Speed} (m \cdot s^{-1}) = \mathrm{SMT}(g \cdot m^{-2} \cdot s^{-1})/ \mathrm{concentration} (g \cdot m^{-3}) \tag{5.1} \]
For a sucrose concentration of 600 mM (or 2.16 x 105 g m-3) and the highest SMT values shown above, Equation 5.1 estimates that phloem sap can move at speeds of up to 56 × 10–5 m s–1 or 200 cm h–1. These estimates have been verified by following the movement of radioisotopes introduced into the phloem translocation stream.
These estimates of transport rates and speeds tacitly assume that phloem sap moves through sieve tubes by mass flow (water and dissolved substances travel at the same speed). Independent estimates of transport rate, concentration of phloem sap and translocation speed lend support to, but do not verify, the assumption that movement occurs as a mass flow.
A simple and direct test for mass flow is to determine experimentally whether water and dissolved substances move at the same speed. This test should be relatively easy to apply using radioactively labelled molecules. Unfortunately, in practice it turns out that different molecular species are not loaded into the sieve tubes at the same rates and the plasma membranes lining the sieve tubes are not equally permeable to each substance. Thus, the analysis is complicated by the necessity to use model-based corrections for rates of loading into and losses from the sieve tubes. Nevertheless, the speed estimates obtained from such experiments are found to be similar for dissimilar molecules, supporting the proposition that mass flow accounts for most transport through sieve tubes.
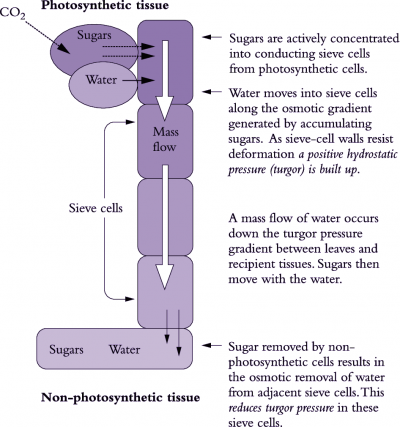
Phloem translocation is generally believed to be driven by pressure. Münch (1930) proposed that a passive mass flow of phloem sap through sieve tubes was driven by the osmotically generated pressure gradient between source and sink regions (Figure 5.11). At source regions, the principal osmotica of phloem sap are actively or passively loaded into sieve tubes from companion cells or mesophyll cells (see 5.3.2), thereby driving water towards the lower water potentials within sieve tubes. As water enters, P rises. Unloading of solutes from sieve tubes at sink regions reverses water potentials; water flows out of sieve tubes and P falls relative to that of sieve tubes in source regions.
The pressure-flow hypothesis can be modelled using the relationship that rate of mass flow (Ff) of a substance is given by the product of speed (S) of solution flow, path cross-sectional area (A) and its concentration (C). That is:
\[F_f = S \cdot A \cdot C \tag{5.2}\]
Speed (m s–1) has the same units as volume flux (Jv — m3 m–2 s–1) of solution passing through a transport conduit. Poisseuille’s Law describes the volume flux (Jv) of a solution of a known viscosity (h) driven by a pressure difference (DP) applied over the length (l) of pathway of radius (r) as:
\[J_v = \pi r^4 \Delta P/8 \eta l \tag{5.3} \]
The term πr4/8ηl in Equation 5.3 provides an estimate of hydraulic conductivity (Lp) of the sieve-tube conduit which is set by the radius of the sieve pores. Raised to the fourth power, small changes in the sieve-pore radius will exert profound effects on the hydraulic conductivity of the sieve tubes (Section 5.2). The viscosity of sieve-tube sap is determined by the chemical species (particularly sugars) and their concentrations in the phloem sap.
Key features of the pressure-flow hypothesis are encapsulated in Equation 5.3. The central question is whether a pressure gradient exists in sieve tubes with the expected direction and of sufficient magnitude to support observed rates of sap flow. Indirect estimates of P in sieve tubes made through determination of intra- and extracellular P support the pressure-flow hypothesis. Direct measurements of sieve-tube P are technically challenging because of the inaccessibility of these small, highly turgid cells. They are, for instance, too small for pressure-probe measurements. However, manometric pressure measurements obtained using severed aphid stylets agree with indirect estimates (Wright and Fisher 1980). Experimental manipulation of the pressure gradient between the source and sink also results in alterations in phloem translocation rates consistent with the pressure-flow model.
Whether the pressure gradient is sufficiently steep is a more vexing question. The pressure gradient required to drive phloem translocation at observed rates is determined by the transport resistance of the phloem path, according to Ohm’s Law. Dimensions of the sieve pores set a limiting radius for volume flux of transported sap (Equation 5.3) and hence transport resistance. If the sieve pores were open and unoccluded by P-protein, a number of studies have demon-strated that the measured pressure gradients are sufficient to support the observed rates of flow. However, the in situ radii of sieve pores remain unknown.
Overall, the pressure-flow hypothesis accounts for many observed features of phloem translocation, including distribution of resources. While conclusive evidence supporting this hypothesis is still sought, less attention is now focused on this issue with a growing appreciation that the phloem pathway has spare transport capacity. Evidence from Kallarackal and Milburn (1984), for example, showed that the specific mass transfer (SMT – see preceding section) to an intact fruit of castor bean could be doubled on removal of competing fruits. Moreover, if P of sieve elements at the sink end of the phloem path was reduced to zero, by severing the pedicel and allowing exudation, SMT rose to an incredible 305 g m–2 sieve-tube area s–1! In another experiment, when half the conducting tissue was removed from the peduncle of sorghum or wheat plants, grain growth rate was not impaired (Wardlaw 1990). Together, these observations imply that phloem has excess carrying capacity in both dicotyledons and monocotyledons. Particularly in monocotyledonous plants, a strong selection pressure for spare transport capacity must exist because there is no vascular cambial activity to replace damaged sieve elements.