Osmosis makes cell expansion possible. Osmotic concepts were first understood by J. Willard Gibbs (1875-76) and demonstrated experimentally soon thereafter by Wilhelm Pfeffer (1876). Neither of these scientists knew how the process caused growth but Pfeffer (1900) sensed that the critical feature was turgor pressure (P). It is now known that P has to be low enough to create a water potential to bring water into the growing cell while at the same time being high enough to expand the wall. This dual role can be understood from the theoretical basis of osmosis (Figure 7.24).
7.3-Ch-Fig-7.24.jpg
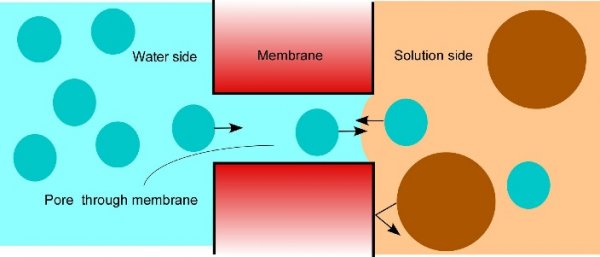
Figure 7.24 How osmosis works. Water is on the left shown as blue dots. An aqueous solution is on the right shown as a mix of blue dots and large brown dots (solute). A porous membrane separates the two compartments but the pores are too small or too selective for the solute to move through. Instead, the solute is reflected by the membrane. The water side contains more water than the solution side because the solute occupies space that otherwise would be occupied by water. Consequently, more water enters the pores from the water side than from the solution side. As long as there is a concentration difference on the two sides of the membrane, more water will cross from the diluter side than from the concentrated side. (Diagram courtesy JS Boyer)
Osmosis in a constrained compartment like a plant cell causes P to build up inside the cell until it becomes high enough to prevent net water entry. At that stage, the cell is in equilibrium with the solution in its surroundings. Inside the cell, P is the turgor pressure and it can be high (positive pressures of 0.5 MPa are common). Outside of the cell in the wall that is hydraulically connected to the xylem, P can vary considerably and tends to be negative during the day because the xylem water is under tension (negative pressure). The tension in xylem is of course transmitted throughout the apoplast. Bearing this in mind, it is possible to express mathematically the osmotic forces and flows across a membrane as:
\[ \frac{dV}{dt} = AL_{p}[(P_i - P_o) - (\Pi_i - \Pi_o)] \tag{1} \]
where V is the net volume of water moving osmotically across the membrane, \(t\) is the time, \(A\) is the area of the membrane, \(P\) is the pressure, \(\Pi\) is the osmotic effect of the solute concentration, \(L_{p}\) is the hydraulic conductivity of the membrane, and subscripts \(i\) and \(o\) refer to the interior (cytoplasm) and exterior (apoplast) of the cell.
It is important to point out that the water potential is \( \Psi = P – \Pi \) and Eq. 1 simplifies to:
\[ \frac{dV}{dt} = AL_{p} \Delta \Psi \tag{2} \]
where \( \Delta \Psi \) is the water potential difference between the inside and outside of the cell. At equilibrium, \(P\) builds until the net flux is zero and Eq. 1 becomes:
\[ (P_i - P_o) = (\Pi_i - \Pi_o) \tag{3} \]
Let’s see how Eq. 3 fits plant cells whose apoplast is hydraulically connected to the xylem. Starting in the xylem where the solution is very dilute (say \(\Pi_o\) = 0) and the wall solution is under tension (say \(P_o\) = -0.7 MPa), osmosis will move water into the cell as long as the cytoplasm is more concentrated (say \(\Pi_i\) = 1 MPa). As water moves in, \(P_i\) builds inside until it prevents water from entering. Ultimately, the \(P_i\) reaches 0.3 MPa whereupon the cell is equilibrated with its surroundings, as shown in Eq. 3 but expressed numerically in Eq. 4:
\[ 0.3 - (-0.7) = (1 - 0) \tag{4} \]
Notice in Eq. 4 that the P difference across the membrane equals the \(\Pi\) difference across the membrane. In other words, the pressure difference is in equilibrium with the osmotic effect of the solute. Of course, if insufficient water can enter the cell to build its turgor as high as 0.3 MPa, \(P_i\) decreases. If it falls near zero, we sometimes see the leaf “wilting”.
A major advantage of the water potential is that it describes the direction of water movement, taking osmotic properties and pressures into account in one symbol. According to the example above (Eq. 4), the water potential outside of the cell is -0.7 MPa (-0.7 + 0.0). Because outside and inside are in equilibrium, the water potential inside of the cell is also -0.7 MPa (0.3 - 1.0). In both places, \(\Psi\) is a negative number (like temperatures below zero).
Osmosis is the key to water entry into the plant. It not only causes water to enter the cells of the plant but also creates the tension in the xylem transmitted to the cell wall (apoplast) that pulls water through the root from the soil. In fact, this ability to pull water from the soil has to balance transpiration. In other words, water uptake by osmosis is necessary to prevent the plant from drying out. Larger \(\Delta\Pi\) create the potential for greater pull extending out into the soil. Wheat typically contains large \(\Pi_i\) (2.0 to 2.5 MPa) that allows it to obtain water from relatively dry soil. Maize generally has small \(\Pi_i\) (1.2 to 1.8 MPa) that makes it less able to obtain water from dry soil. Maize tends to be less drought tolerant than wheat. The reasons for the \(\Pi_i\) differences are unknown.
These ideas work for osmosis in plant cells that discriminate perfectly between solute and water (water moves through the membrane but solute does not). In healthy cells, most membranes are nearly perfect and negligible solute moves through (solute actually moves through on specific carriers but the amount is negligible osmotically). If solute crosses the membrane, it acts essentially the same as a water molecule, and the osmotic force Π is diminished. Places where this may happen are phloem termini where large amounts of solute are delivered to the developing embryo along with water. Developing grain would be an example. Another place is in air-dry seeds whose membranes have been dehydrated and are leaky to solute until the cells are rehydrated during imbibition, allowing the membranes to re-form.
So far, we have only considered the hydraulic conductivity of membranes of individual cells. Sometimes it might be useful to determine the conductivity of a whole organ such as a root system or leaf. For that an abbreviated form of Eq. 1 is typically used:
\[ \frac{dV}{dt} = L(\Delta\Psi) \tag{5} \]
where \(L\) is called the water conductance of the organ and the definition of the other terms remains unchanged. The reason we cannot use Eq. 2 is that the area for flow is not the plasma membrane of the cell. In effect, \(A\) is undefined and is included in \(L\) but the general principle governing flow is otherwise like that in Eq. 2. As you can see, the bigger the root system the higher the flow and thus \(L\) will tend to get larger as the organ grows.